Simple Harmonic Motion

Claimed for editing by Elton Leander Pinto 10/29/2018

This is a type of periodic motion in which, from a physical point of view, a restorative force acts to always bring back the oscillating particle back to its equilibrium position. An example of a system exhibiting this kind of behavior includes a pendulum oscillating in a medium that provides minimal resistance to motion. However, most oscillating systems that we observe in our day-to-day life are not perfect simple harmonic oscillators. Simple harmonic motion is an approximation that ignores friction and air resistance. Although this assumption can often not be made in everyday calculations, simple harmonic motion can approximate these otherwise complicated situations, fairly well. This is because of the effect of damping on the motion of systems that reduces the amplitude of oscillation, and hence we get what is known as damped oscillations. Another interesting idea that is relevant when we talk about these systems is the concept of resonance, and how it can be exploited to bring about astonishing results. Simple harmonic motion can be used to estimate many systems including spring-mass systems and the swinging of a pendulum in certain instances which will be explained in further detail below. We will explore these ideas in the following section.

The Main Idea

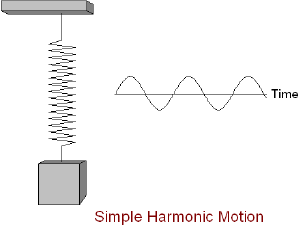
Simple harmonic motion is a periodic motion, a motion that is repeated over some time interval. This periodic motion has a restoring force, a force that is always working to return the system to equilibrium position, that is proportional and opposite to displacement. Due to this as the system gets farther from equilibrium position the larger the force is to return it to equilibrium position. When no friction or air resistance is present the system will continue to oscillate as the restoring force decreases as the object gets closer to equilibrium position until the force reaches zero, but at which point the particle continues due to its initial momentum until passes equilibrium position. Then the restoring forces increases in the opposite direction until the momentum is changed enough to change the direction of the particle and the process repeats. A common example of simple harmonic motion is an undamped spring-mass system, or one that does not proceed to rest due to friction or another dissipative force.

A Mathematical Model

Simple harmonic motion occurs very frequently in our treatment of physical systems, and is a useful approximation for many because it is often reasonably accurate, and because we have the tools to describe it exactly. We may consider the example of the spring (see fig) to arrive at a general equation for simple harmonic motion, and tweak its parameters to obtain an equation that is well suited to describe the oscillatory motion of spring-mass systems. If we are to pull the mass a tad bit away from its equilibrium position and then let go, we see that the spring-mass system seems to undergo some kind of periodic motion. To find a mathematical representation for such a motion, we may draw an analogy between this behavior and the mathematics at our disposal. After a fixed period of time, we will find the system returns to its original state. Use of terminology such as period should remind one of precalculus, and specifically of the sinusoidal functions sine and cosine. Let us suppose then that the position can be described by a cosine function (we choose cosine instead of sine by convention, since in other methods of derivation it is more convenient to choose one over the other). We also know from observing the motion of the object that its position depends upon the frequency and amplitude of oscillations. Hopefully you remember how to parameterize a circle: we define [math]\displaystyle{ x = R\cos(t) }[/math] and [math]\displaystyle{ y = R \sin(t) }[/math], where [math]\displaystyle{ R }[/math] is the radius, and we take [math]\displaystyle{ t }[/math] from 0 to [math]\displaystyle{ 2\pi }[/math]. However, we could just as easily assume that [math]\displaystyle{ t }[/math] keeps going past [math]\displaystyle{ 2\pi }[/math], or that it takes on negative values, since it will stay on the circle; we just know that it will trace out a circle over a period of [math]\displaystyle{ 2\pi }[/math]. By this same token, we can also choose to give [math]\displaystyle{ t }[/math] a coefficient, writing the equations as [math]\displaystyle{ x = R\cos(2\pi t) }[/math] and [math]\displaystyle{ y = R\sin(2\pi t) }[/math]. Then the circle will be traced out as [math]\displaystyle{ t }[/math] goes from 0 to 1. If we were to make the coefficient [math]\displaystyle{ \pi }[/math] instead, then [math]\displaystyle{ t }[/math] would go from 0 to 2. Thus its period would be twice as large. All of this guides how we will now write out the equation for a spring. We know that the period will affect the argument inside the cosine, and the distance it travels will be determined by the coefficient outside. Calling the maximum distance the system will extend the amplitude, [math]\displaystyle{ A }[/math], and calling the inverse of the period the frequency, [math]\displaystyle{ f }[/math], we have the generic equation

[math]\displaystyle{ x(t) = A \cos(2\pi f t) }[/math]

By further convention, we'll rewrite this in terms of angular frequency [math]\displaystyle{ \omega = 2 \pi f }[/math], giving

[math]\displaystyle{ x(t) = A \cos(\omega t) }[/math]

We may also generalize this to assume that it does not start at maximum extension, by introducing a phase factor [math]\displaystyle{ \phi }[/math]

[math]\displaystyle{ x(t) = Acos(ωt + φ) }[/math]

Now let us consider the prominent example of a Hookean spring. The force of an ideal spring-mass system can be found using [math]\displaystyle{ \vec{F}={-k}*\vec{s} }[/math] where [math]\displaystyle{ \vec{s}=\vec{L}-{\vec{L}_{o}} }[/math]. This equation stems from Newton's Second Law and Hooke's Law which is a first order linear approximation for forces acting on an elastic system, such as a spring. The solution to this differential equation is [math]\displaystyle{ x=A\cos(\omega t + \phi) }[/math] where [math]\displaystyle{ ω=\sqrt{k/m} }[/math]. Combining this equation with our knowledge of sinusoidal functions, we define the period of oscillation to be [math]\displaystyle{ T=2π/ω }[/math].

Advanced: Derivation with Differential Equations

Our differential equation is given by Hooke's Law and Newton's Second Law:

[math]\displaystyle{ x''(t) = -\frac{k}{m}x(t) }[/math]

This is a very nice equation (it is linear and homogeneous), so we may solve it by creating a linear combination of two known solutions. As it happens, we know two functions that can solve this equation: [math]\displaystyle{ x_1(t) = a\cos(\omega t) }[/math] and [math]\displaystyle{ x_2 (t) = b\sin(\omega t) }[/math]. Then any solution may be written as

[math]\displaystyle{ x(t) = a \cos(\omega t) + b\sin(\omega t) }[/math]

Now, to make this a convenient form, lets call [math]\displaystyle{ A = \sqrt{a^2 + b^2} }[/math], and pull it out, giving

[math]\displaystyle{ x(t) = A\biggr{(} \frac{a}{A} \cos(\omega t) + \frac{b}{A}\sin(\omega t) \biggr{)} }[/math]

By construction, these fractions look a lot like the definition of cosine and sine from trigonometry, and so we call them these respectively. Now, we can use to reduce this to

[math]\displaystyle{ x(t) = A \cos(\omega t + \phi) }[/math]

Now, we want to determine the constants. If the initial velocity is zero, this is easy: [math]\displaystyle{ A = x_i }[/math] and [math]\displaystyle{ \phi = 0 }[/math]. Otherwise, however, we will need to use the initial value conditions:

[math]\displaystyle{ x(0) = A \cos(\phi) }[/math]

[math]\displaystyle{ x'(0) = A\omega \sin(\phi) }[/math]

Taking a ratio of these two and solving for [math]\displaystyle{ \phi }[/math] will lead to

[math]\displaystyle{ \phi = \arctan\biggr{(}\frac{x'(0)}{\omega x(0)}\biggr{)} }[/math]

Finally, this may be substituted into either equation to solve for [math]\displaystyle{ A }[/math]

A Computational Model

Simple harmonic motion in vPython uses glowscript to implement a varying force iterative motion predictor, while this has uses numpy to do the same (here the cell with simp_harm_func is the one we wish to look at). For a detailed description of how varying force computational methods work, see Fundamentals of Iterative Prediction with Varying Force. The important distinction of simple harmonic motion is that it is defined by the force function

[math]\displaystyle{ F(t,x,v) = -kx }[/math]

Where by convention we have [math]\displaystyle{ k \gt 0 }[/math].

Examples

Simple

Problem: A spring has a restoring force of 300 N when it is stretched -.2m. What is the spring's constant [math]\displaystyle{ {K_{s}} }[/math]. in N/m?

Solution

[math]\displaystyle{ F={-K_{s}}*s }[/math]

[math]\displaystyle{ {-K_{s}}=F/s }[/math]

[math]\displaystyle{ {-K_{s}}=300N/-.2m }[/math]

[math]\displaystyle{ {K_{s}}=1500N/m }[/math]

Middling

Problem: What is the oscillation period of a spiring with spring constant 15N/m with a 30 kg mass attached?

Solution

[math]\displaystyle{ T=2π/ω }[/math] or [math]\displaystyle{ T=2π√(m/{K_{s}}) }[/math]

[math]\displaystyle{ {K_{s}}=15N/m) }[/math] and [math]\displaystyle{ m=30kg }[/math]

[math]\displaystyle{ T=2π√(30kg/15N/m) }[/math]

[math]\displaystyle{ T=8.88 seconds }[/math]

Difficult

Problem: A spring with spring constant 18 N/m has mass of 2 kg is attached to it. The mass is then displaced to x = 2 . How much time does it take for the block to travel to the point x = 1?

Solution:

Solution

[math]\displaystyle{ x=Acos(ωt) }[/math]

[math]\displaystyle{ x/A=cos(√({K_{s}}/m)t) }[/math]

[math]\displaystyle{ 1/2=cos(√(18N/m/2kg)t) }[/math]

[math]\displaystyle{ cos^{-1}(1/2)=3t }[/math]

[math]\displaystyle{ t=.35seconds }[/math]

Damping

We know from our observations of say a pendulum swinging or a spring bobbing that it's periodic motion eventually dies out. This is due to the dissipative forces prevalent in nature (air resistance and viscous drag ) that dissipate the potential and kinetic energies of the system (spring+mass) to the surroundings (everything outside our chosen system ) into other forms of energy (heat, sound, etc.). When this happens, we say that the system is executing damped oscillations.

It takes some hairy math to arrive at an approximate analytical solution for the above case. Instead of doing that, however, it is much easier for us to encode the presence of dissipative forces if we were to carry out numerical integration using an iterative process.

Whenever we calculate the net force on the mass during the iterative process, all we have to do now is add a force that is representative of any of the dissipative forces. If we are dealing with air resistance, then we can use the equation

[math]\displaystyle{ \vec{F} = -0.5CAρv^2\hat{v} }[/math]

Else, we can use this equation

[math]\displaystyle{ \vec{F} = -b\vec{v} }[/math] where b is the damping constant

Connectedness

One interesting application of simple harmonic motion is its ability to approximate the interatomic vibration of molecules which I find very interesting as an Earth and Atmospheric Science major, trying to better understand our environment and how the molecules it is made up of interact. I have always been very intrigued by the composition and interactions of molecules and this approximations brings me another step closer to understanding how our world works. An interesting industrial application of simple harmonic motion is its approximation of a car running on worn down shock absorbers.

History

Thomas Hooke, an English scientist, created Hooke's Law in 1660 while working on his invention the watch-spring. In the 1660s Hooke gained the title of curator of the Royal Society where he led top experiments for the society. The watch-spring Hooke was working on was one of the first capable of determining longitude at sea by using a spring in simple harmonic motion which has a tendency resist disturbances such as the shakes that could occur while at sea.

See also

Hooke's Law

External links

https://www.khanacademy.org/science/physics/oscillatory-motion/harmonic-motion/v/introduction-to-harmonic-motion

http://hyperphysics.phy-astr.gsu.edu/hbase/shm.html

https://en.wikibooks.org/wiki/A-level_Physics_(Advancing_Physics)/Simple_Harmonic_Motion/Mathematical_Derivation