Gravitational Force in Space and Other Applications: Difference between revisions
| Line 24: | Line 24: | ||
::<math> F_{net}=\frac{mv^2}{r}= \frac{Gm_{1}m_{2}}{r^{2}} </math> | ::<math> F_{net}=\frac{mv^2}{r}= \frac{Gm_{1}m_{2}}{r^{2}} </math> | ||
Through simple manipulation of this net force, we can determine that the period (which is equal to <math>\frac{2\ | Through simple manipulation of this net force, we can determine that the period (which is equal to <math>\frac{2{\pi}r}{v}</math>) squared is proportional to the radius cubed. While this is just a simple derivation for a circular orbit, the same holds true for elliptical orbits, and, in fact, when you use years for the units of period, and astronomical units (1 AU = the distance from the Earth to the Sun) for the semi-major axis (''a''), the following equation holds true for the solar system: | ||
::* <math>P^2=a^3</math> | ::* <math>P^2=a^3</math> | ||
Revision as of 14:00, 14 June 2019
This page looks into the gravitational force in space, and other applications of the gravitational force. Kepler's Laws are also explained here.
Main Idea
The gravitational force, as it acts in space, can be used to explain the motions of celestial bodies, and thus is of extreme interest when predicting future events in our Solar System.
Johannes Kepler, prior to Newton, had created laws to explain the motion of celestial bodies. His laws, explained below, were further proven by Newton's idea of gravity, which can explain why these laws are true.

- Kepler's first law states that all planets move about the Sun in an elliptical orbit, with the Sun at one of the foci of the ellipse. This can be further elaborated to say that every body orbits around the center of mass in its system on an elliptical orbit. For example, in the Earth-Moon system, the Moon orbits around the Earth in an elliptical orbit, with the Earth at one of the foci of the ellipse. An ellipse, in this case, can be a circle, oval, parabola, or hyperbola, depending on the type of motion of the orbiting body. The gravity of the Sun keeps the object bound on the orbit, with the force of gravity always pointing radially inwards towards the Sun. This constantly changing direction of gravitational force is what keeps the planet bound.

- Kepler's second law, the law of equal areas, states that a planetary body sweeps out an equal area in its orbit in equal time. This is also shown in a diagram. Basically, if you draw a line from the planet to the Sun, the area that is created in some time segment by the motion of the planet will be the same as the area created in an equivalent time segment at a different point in the objects orbit. This can also be explained by the gravitational force, and the conservation of angular momentum, which will be covered later in the course.
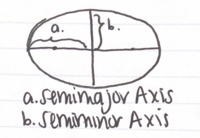
- Kepler's third law states that the square of the orbital period of the planet (the time it takes to go around the Sun) is directly proportional to the cube of its semi-major axis (which is half of the length of the longer axis of the ellipse, and is shown in a diagram). This law is incredibly useful, especially in determining the semi-major axis of exoplanets when we know their period from transits (it can be detected when the planet passes in front of the star. By measuring the timing of these transits, the period of the planet can be determined).
A Mathematical Model
The easiest of Kepler's three laws to formulate mathematically is Kepler's 3rd Law. By setting the net force equal to the gravitational force, we can derive a simple equation for the period of the planet.
- [math]\displaystyle{ F_{net}=ma=\frac{Gm_{1}m_{2}}{r^{2}} }[/math]
In a circular orbit, the acceleration of planet is equal to the square of its velocity over the radius of the orbit. This will be further explained later, when the centripetal force is covered, but for this purpose, we can accept this relationship and replace ma in our equation.
- [math]\displaystyle{ F_{net}=\frac{mv^2}{r}= \frac{Gm_{1}m_{2}}{r^{2}} }[/math]
Through simple manipulation of this net force, we can determine that the period (which is equal to [math]\displaystyle{ \frac{2{\pi}r}{v} }[/math]) squared is proportional to the radius cubed. While this is just a simple derivation for a circular orbit, the same holds true for elliptical orbits, and, in fact, when you use years for the units of period, and astronomical units (1 AU = the distance from the Earth to the Sun) for the semi-major axis (a), the following equation holds true for the solar system:
- [math]\displaystyle{ P^2=a^3 }[/math]