Introduction to Magnetic Force

This page provides a short introduction to the concept of the magnetic force.

Main Idea

The magnetic force acts upon moving charges (or currents). This means that the magnitude of the magnetic force has a direct dependence on the velocity of the charge it is acting upon. Furthermore, the magnetic force acts via the magnetic field. This magnetic force acts in a direction perpendicular to both the velocity of the charge and the direction of the magnetic field.

The magnetic field is a vector field (meaning that it extends in all three dimensions). Magnetic fields are provided most simply either by moving charges or by dipoles. When the magnetic field strength is known, it makes finding the magnetic force quite simple.

Magnetic fields and electric fields are, in fact, related, and both together comprise the electromagnetic force. This force is the second strongest of the four fundamental forces, behind the nuclear strong force, and ahead of the weak force and the gravitational force.

A Mathematical Model

Magnetic force can be represented as follows, where q is the charge on a particle, v is that particles velocity, and B is the magnetic field. Here, [math]\displaystyle{ \theta }[/math] represents the angle between the velocity and magnetic field vectors. The direction of the magnetic field can be found using the right hand rule.

• [math]\displaystyle{ \vec{\mathbf{F_B}}=q\vec{\mathbf{v}}\times{}\vec{\mathbf{B}} }[/math]
• [math]\displaystyle{ |\vec{\mathbf{F_B}}|=qvBsin(\theta{}) }[/math]

The above means that any particle at rest will NOT experience any magnetic force.

The magnetic force also applies to a current carrying wire. Because a current is essentially made of moving charges, this means that the current carrying wire will experience a force. This force is directly proportional to the length of the wire and the current in that wire, as is displayed below. Here I is the magnitude of the current, which is in units amperes, or Coulombs/second, l is in units of length, and is in the same direction as the current (for the cross product).

• [math]\displaystyle{ \vec{\mathbf{F_B}}=I\vec{\mathbf{l}}\times{}\vec{\mathbf{B}} }[/math]
• [math]\displaystyle{ |\vec{\mathbf{F_B}}|=IlBsin(\theta{}) }[/math]

Examples

Simple

Say you have a 1 C charge moving at a rate of 3 m/s. This velocity makes an angle of 60 degrees with respect to a magnetic field with strength 2 Tesla. What is the magnitude of the force the charge experiences?

The units given in the problem statement are all proper SI units, and so the numbers can just be plugged in to the following equation:

[math]\displaystyle{ F_B=qvBsin(\theta{}) }[/math]

[math]\displaystyle{ F_B=(1 C)(3 m/s)(2 T)(sin(60))=5.196 N }[/math]

Thus the answer to this problem is, straightforwardly, 5.196 N.

Middling

A diagram depicting the problem for the middling section. Here, the magnetic field is going out of the page.

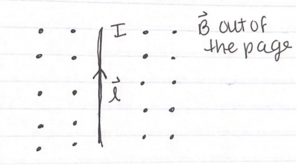
Suppose you have a wire with a current I=6 amps. This wire is sitting in a constant magnetic field of magnitude 1 T. This wire has length 6 cm. What is the magnitude and the direction of the force acting upon the wire, according to the diagram? The magnetic field is pointing out of the page.

The easiest first step would be to determine the direction of the magnetic force. By using the right hand rule, we can determine that when the current length, which is going up, is crossed with a vector pointing out of the page, the resulting vector would point towards the right, in the so-called positive x-direction.

Next, we can determine the magnitude of the resultant force via the following relation. Because [math]\displaystyle{ \theta{} }[/math] here is equal to 90 degrees, [math]\displaystyle{ sin(\theta{}) }[/math] is equal simply to one.

• [math]\displaystyle{ F_B=IlBsin(\theta{}) }[/math]
• [math]\displaystyle{ F_B=(6A)(0.06m)(1T)=0.36N }[/math]

Finally, as stated before, we know that this is solely in the positive x-direction due to the right hand rule.