SI Units

This page describes the International System of Units and lists its units.

The Main Idea

The International System of Units is a set of units allowing for the quantification of each physical dimension. It was invented in France as an extension of the metric system under the name "Système Internationale d'Unités," which is why it is abbreviated to "SI". SI Units are practically universally used for scientific applications, and are used in most countries in everyday life as well, although the United States, which uses customary units, is a notable exception.

The International System of Units has seven base units with specific definitions and countless derivative units which are created by multiplying and dividing the base units. For example, the meter (m) is the base unit for the dimension distance and the second (s) is the base unit for the dimension time. The meter per second (m/s) measures the dimension speed and is a derivative unit because it can be obtained by dividing the meter by the second.

Because measurements must often be made on many different scales, the International System of Units also defines a variety of prefixes for use with its units. The prefixes scale the values of each unit by multiples of 10 and 1/10. For example, the kilometer is 1000 times as long as the meter because of the prefix "kilo."

The International System of Units is versatile and can change over time to meet the evolving needs of scientists. Over the last several centuries, the number of base units has grown from 3 to 7 as a result of the discovery of new dimensions that could not be expressed in terms of existing base units. The number of derivative units recognized as meaningful has also grown substantially and will likely continue to as the human understanding of the physical world improves. Additionally, the seven base units have undergone redefinition at several points in time, most recently on May 20 2019. The purpose of each redefinition is not to change the units' values (in fact, their values are changed as little as possible), but to make their definitions more universally constant and reproducible.

The Seven Base Units

The values of the seven base units are historically motivated, but most of their current definitions have been changed from the original. Today, each of the 7 base unit is defined by fixing a specific natural universal constant to a certain numerical value.

Second (s)

The second measures time.

Today, the second is defined by fixing the value of the cesium hyperfine transition frequency [math]\displaystyle{ \Delta v_{Cs} }[/math] to equal exactly 9192631770 hz (transitions per second). This defines the second as the 9192631770 times the period of the transition between the two levels of the ground state of cesium-133 atom. Atomic clocks make use of this phenomenon by counting the cesium transitions as a mechanism for keeping time! This definition was instated in 1967.

The second was initially defined as a fraction (1/86400) of a day of 24 hours of 60 minutes of 60 seconds. This definition is poor primarily because the duration of the day changes slightly over time. In 1956 the second was defined as 1/31556925.9747 of the tropical year. (The tropical year is the time it takes the sun to return to the same position in the season cycle, which is about 20 minutes shorter than the causal year.) However, this is still not as elegant as the current definition because it is based on our particular solar system, which may not always exist or be available for measuring.

Meter (m)

The meter measures distance.

Today, the meter is defined by fixing the value of the speed of light in a vacuum [math]\displaystyle{ c }[/math] to equal exactly 299,792,458 m/s. Since the second is already defined, this defines the meter as the distance traveled by light in a vacuum in 1/29979248^th of a second.

The meter was originally defined in 1973 as 1/10,000,000 of the meridian through Paris between the North Pole and the Equator. In 1960 it was redefined as 1650763.73 wavelengths of the radiation in a vacuum corresponding to the transition between 2p10 and 5d5 transition levels of the krypton-86 atom.

Kilogram

The kilogram measures mass.

Today, the kilogram is defined by fixing the value of Planck's constant [math]\displaystyle{ h }[/math] to equal exactly 6.62607015×10−34 J s. Recall that the joule is not a base unit, but a derived unit equal to the kg m²/s². Since the meter and the second are already defined, this leaves only one possible value for the kilogram. This definition was instated as part of the SI unit redefinition of May 20, 2019.

In 1973, the SI unit for mass was called the grave. It was defined as being the mass of 1 liter of pure water at its freezing temperature. Later, in 1889, it was redefined as the mass of a specific sample a platinum alloy. The sample is called "Le Gran K" and is kept in a temperature-controlled vault just outside of Paris, France. This definition was inadequate because it was not universally reproducible.

Ampere

The ampere measures electrical current.

Today the ampere is defined by fixing the value of the elementary charge [math]\displaystyle{ e }[/math] to be exactly 1.602176634e-19 C. This defines the Coulomb, and since an ampere is 1 Coulomb per second (and the second is already defined), it also defines the Ampere.

In 1881, the ampere was defined as a tenth of the current required to create a magnetic field of one Oersted at the center of a 1cm arc of wire with curve radius 1cm. In 1946, the ampere was defined as the current required to create a force of 2e-7 Newtons per meter of length between two straight parallel conductors of infinite length placed 1m apart in a vacuum.

Kelvin

The Kelvin measures temperature.

Today, the Kelvin is defined by fixing the value of the Boltzmann constant [math]\displaystyle{ k }[/math] equal to exactly 1.380 649 x 10–23 J/K.

Mole

The mole measures the amount of a substance present by number of particles.

Today, the mole is defined by fixing the value of the Avogadro constant [math]\displaystyle{ N_A }[/math] equal to exactly 6.022140857 × 10²³ mol^-1. This defines the mol to be 6.022140857 × 10²³ mol particles.

The mol was originally defined in 1967 the mole as the number of carbon-12 atoms necessary to comprise a 12 gram sample.

Candela

The candela measures luminous intensity.

A candela is currently defined by fixing the value of the luminous efficacy constant [math]\displaystyle{ K_{cd} }[/math] to equal exactly 683 lumens per watt. This defines the candela as the luminous instensity of a source that emits radiation of a frequency 5.4e14 Hz in 1/683 of a steradian. (A steradian is the 3D analog for the radian; it is a part of the sphere's surface area equalling the radius squared in area.) This is about the luminous intensity of a candle.

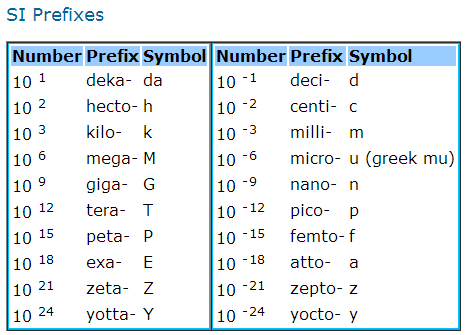
Prefixes

Mass, length or any numbers in physics can be very small or very large. Electrons can be a great example. The mass of electron is 0.0000000000000000000000910938356g or 9.10938356 E-31. In SI, prefixes are available to adjust the size of a unit so as to keep the number of those units reasonable. It is kind of difficult to read that number in word. However with the prefix it can be. Image below shows the list of prefixes.

These prefixes are incredibly useful for clarity purposes. The prefixes listed are incredibly useful for a speaker or writer in order to help ease their use.

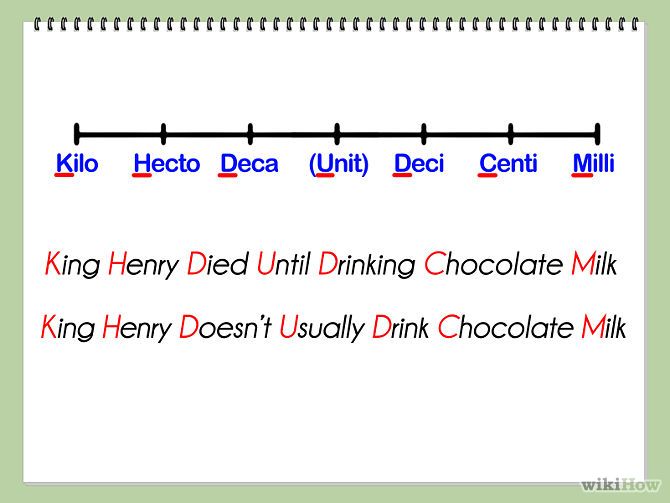
Here is a video that helps to explain the prefixes and an easy way to remember:

Easy Way to Memorize Metric Prefixes

Derived SI units

This image above shows the relationships between many units used in physics based on base SI units. As we can see, most of the units in physics is related to the SI units. It is because there are many quantities that cannot be expressed by a single base SI unit. For example, when talking about the density, it is volume/mass. Mass has it's own SI unit which is a gram. However volume doesn't. Volume is expressed with derived SI unit, meters cubed. As a result, unit for density is [math]\displaystyle{ \mathrm{m}^3/\mathrm{g} }[/math] . Those units are called derived SI units. Units can be combined to create new unit. Some frequently-used combinations have their units named. Here are some examples:

• Watt (W), the unit of power.
  • [math]\displaystyle{ \mathrm{W} = \mathrm{J}/\mathrm{s} \ }[/math]

• Pascal (Pa), the unit of pressure.
  • [math]\displaystyle{ \mathrm{Pa} = \mathrm{N}/\mathrm{m}^2 \ }[/math]

• Hertz (Hz), the unit of frequency.
  • [math]\displaystyle{ \mathrm{Hz} = 1/\mathrm{s} = \mathrm{s}^{-1} \ }[/math]

• Newton (N), the unit of force.
  • [math]\displaystyle{ \mathrm{N} = \mathrm{kg} \cdot \mathrm{m}/\mathrm{s}^2 }[/math]

• Joule (J), the unit of energy.
  • [math]\displaystyle{ \mathrm{J} = \mathrm{N} \cdot \mathrm{m} = \mathrm{kg} \cdot \mathrm{m}^2/\mathrm{s}^2 }[/math]

• Coulomb (C), the unit of electric charge.
  • [math]\displaystyle{ \mathrm{C} = \mathrm{A} \cdot \mathrm{s} }[/math]

• Volt (V), the unit of electric potential or voltage.
  • [math]\displaystyle{ \mathrm{V} = \mathrm{J}/\mathrm{C} = \mathrm{W}/\mathrm{A} \ }[/math]

The list is incredibly useful for measuring quantities that do not have a standard SI unit already in place. These calculations are used frequently to find further derived SI Units in complex equations.

Examples of Calculations Using SI Units

Connectedness

This topic can be applied to every aspect of science. When solving the problem, or even when doing research, every equation and theory is based on SI units. It is a promise between scientists that they will use these certain units to reduce errors or misunderstanding. Therefore, it is very important to know the concept of SI units. This topic is connected to not only physics but also every other scientific subject. In addition, it might not be familiar in the United States, but in most other countries, they use SI units in ordinary life. SI units create a form of standardization throughout the scientific community. This standardization stems from their connection to fundamental constants. These constants are dependent on naturally occurring laws on Earth. As a result, since these units are connected to these constants that are unchanging no matter what location on Earth they're being observed at, this system of measurement is able to achieve a high level of standardization. This establishes a sense of unity and allows scientists to be on the same page no matter what nationality they are. It's through the use of these units by the community of scientists as a whole that error can be reduced to a minimum and calculations and findings can be standardized across the globe. SI units also allow scientists to reproduce experiments and record their results in the same form. This allows for more credibility among findings as well. SI units are also very useful for the use of dimensional analysis. Dimensional analysis is the mathematical problem solving method that essentially means that any number expression can be multiplied by another and its inherent value won't be changed. This vital problem solving idea is possible due to the fact that SI units can be converted to non SI units with incredible ease. SI units create an incredible amount of standardization throughout the scientific community and have been essential for the production of viable and credible scientific results.

Due to recent events in the scientific community and the new levels of accuracy achieved from the use of modern and scientifically advanced equipment, there have been several discoveries that can redefine how we understand fundamental constants. Since SI units are closely intertwined with fundamental constants, these discoveries have great relevance. Most of these discoveries are in the field of quantum physics which is a new field in comparison to other scientific subjects. The technology age has given scientists cutting-edge equipment allowing them to reach results that are more specific and accurate than ever before. For example, this equipment can allow them to calculate a more accurate mass of an electron, which is an important constant and affects the values of base units in the SI unit system. When discoveries like these directly affect our understanding of fundamental constants, they can have an effect on the SI unit system. However, some discoveries, but not all, might only change the value of a constant by a minuscule amount, so the SI units will barely change their values and will most likely not directly affect the way most students solve problems since they will tend to round in problems.

History

The Metric System was created around the time of the French Revolution and the subsequent deposition of two platinum standards representing the meter and the kilogram, on 22 June 1799, in the Archives de la Republic in Paris can be seen as the first step in the development of the present International System of Units. Each of the base units has root within the physical world. For example the unit of metre is derived from dimensions of the Earth, the kilogram was derived the volume of of one liter of water. These 2 units are the baseline for the remainder of the SI system. The new metric system was originally abandoned by France. In 1837, the metric system was readopted by France, and slowly then became adopted by the scientific community. After this a man named James Clerk Maxwell presented the idea of a number of base units, time, mass, and length. This 3 base units could then be used to derive a series of other measurements throughout the scientific world. However it was quickly discovered that these units cannot describe non-mechanical properties. Most importantly they couldn't properly describe the electrical properties of the world. A man named Giovanni Giorgi, an Italian physicist and electrical engineer, proposed a fourth base unit should be added to the original 3 in order to properly describe the electrical systems of the world. This unit was later decided, in 1935, to be the ampere thus allowing the world to aptly describe electrical systems as well. As the years passed these units began to become more and more commonplace among the world, with many other countries beginning to use the SI system as their main form of measurement. The SI system quickly became the accepted scientific measuring system as well. The use of this system has helped to advance and drive scientific advancement throughout the years.

Furthermore, the SI unit system was established in 1960 by the 11th General Conference on Weights and Measures. The CGPM is the international authority that ensures wide spread of the SI system, and it modifies the SI system as necessary to reflect the latest advances in science and technology. The General Conference receives the report of the International Committee for Weights and Measures on work accomplished. It discusses and examines the arrangements required to improve the International System of Units (SI). It also then endorses the results of new fundamental determinations and various scientific resolutions and applies them to an international scope. It further decides all major issues concerning the development of the organization as a whole.

Further reading

SI Units for Clinical Measurement 1st Edition by Donald S. Young

Matter & Interactions, Vol. I: Modern Mechanics, 4nd Edition by R. Chabay & B. Sherwood (John Wiley & Sons 2015)

Base units of the SI, fundamental constants and modern quantum physics by Christian J Bordé

References and External Links

http://physics.nist.gov/ National institute of standards and Technology.

http://wps.prenhall.com/wps/media/objects/165/169061/blb9ch0104.html Pearson educational site.

Matter & Interactions, Vol. I: Modern Mechanics, 4nd Edition by R. Chabay & B. Sherwood (John Wiley & Sons 2015)

Tutorial & Drill Problems for General Chemistry (and Intro) By Walter S. Hamilton, Ph.D.

Base units of the SI, fundamental constants and modern quantum physics By Christian J Bordé, Published 15 September 2005

https://www.youtube.com/embed/h04x3Vr2GGE

https://www.youtube.com/watch?v=ZMByI4s-D-Y

https://www.youtube.com/watch?v=c_e1wITe_ig&t=521s

https://www.youtube.com/watch?v=YmCrFPC1qi4

https://www.bipm.org/en/measurement-units/