Resonance

Resonance

Resonance is the physical phenomenon in which a system vibrates in response to an applied frequency, but the external force of this frequency interacts with the object in such a way that it causes the system to oscillate with a maximum amplitude due to the specific frequency induced. This property applies to many fields of physics when studying the way an object behaves in certain situations.

Natural Frequencies

When dealing with sound and its interaction with various objects in space, a resonant frequency of a wave is the natural frequency of vibration determined by the physical and chemical properties of said object.The existence of resonance in and of itself depends on the existence of natural frequencies. Objects often have multiple natural vibrating resonant frequencies, and it will pick out those frequencies from a series of excitations, making it an even more useful tool when identifying the properties of an object.

History

One of the most famous visible examples of resonance in history is the disaster at the Tacoma Narrows Bridge in 1940. This bridge, in Tacoma, Washington, spanned the Tacoma Narrows Strait, but it collapsed into the waters of Puget Sound on November 7, 1940.

This is the bridge during its collapse in 1940.

This bridge had such a short lived existence due to resonance. Since its construction, workers observed vertical movement in the suspension bridge on windy days. This brought about the origin of the bridge's nickname: "Galloping Gertie". However, on a particularly windy day, the wind provided the bridge with a periodic vibrating frequency that matched the bridge's natural vibrational frequency, causing the bridge to become a massive oscillating standing wave. This intense oscillation proved too much for the structural integrity of the bridge, and it collapsed. No human lives were lost in the accident, but a black, male cocker spaniel named Tubby passed away from the incident.

Standing Waves

Studying resonance requires knowledge of what a standing wave is and how it behaves because resonance within objects have patterns of this nature. A standing wave is formed when two waves propagate through a medium and experiences both constructive and destructive interference with each other when reverberating off of a barrier.

This is a standing wave with labeled nodes and antinodes

This interference causes some areas of the medium to always appear still, while other areas of the medium are oscillating. These areas are called nodes and antinodes. A node is the term used to describe a place where the medium does not move due to the vibration. On the other hand, an antinode is the point where the maximum displacement of the medium occurs due to the vibration of the wave. An important characteristic of a standing wave is that when the wave reaches a fixed barrier at the end of the propagation medium, it changes phase and travels in the reverse direction instead of continuing forward. In that, a change in phase means a 180 degree transformation in the period of the wave. This can be more easily understood when viewed in the visuals provided below.

Harmonics

Wave patterns occur in specific manners based on the certain frequency applied. The frequencies of the wave and their relative patterns are called harmonics. Harmonics behave in a way that provides a convenient mathematical model based on the wavelength of the wave, the harmonic type, and the length of the medium it is propagating through.

First (Fundamental), second, third, fourth, and fifth Harmonics.

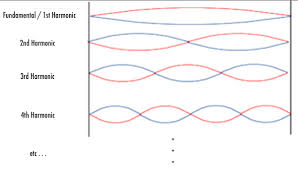
The first harmonic consists of a single antinode in the middle of the medium, and this antinode oscillates up and down continuously. Next, the second harmonic creates two antinodes and three nodes. A full wavelength can be observed here. The third harmonic consists of three antinodes and four nodes. From these progressive patterns, a mathematical relationship can be derived to calculate the length of medium based on the wavelength of the wave. This relationship can be seen below.

A Mathematical Model

First Harmonic - [math]\displaystyle{ L = \frac{1}{2} * \lambda }[/math]

Second Harmonic - [math]\displaystyle{ L = (2/2) * \lambda }[/math]

Third Harmonic - [math]\displaystyle{ L = (3/2) * \lambda }[/math]

Fourth Harmonic - [math]\displaystyle{ L = (4/2) * \lambda }[/math]

.

.

.

nth Harmonic - [math]\displaystyle{ L = (n/2) * \lambda }[/math]

References

https://www.grc.nasa.gov/www/k-12/airplane/thermo0.html http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/thereq.html https://www.grc.nasa.gov/www/k-12/airplane/thermo2.html http://www.phys.nthu.edu.tw/~thschang/notes/GP21.pdf http://www.eoearth.org/view/article/153532/

Sound