Point Charge: Difference between revisions

Revision as of 11:47, 22 November 2019

This page is all about the Electric Field due to a Point Charge.CLAIMED BY JENNIFER YU 09/06/19 (Fall 2019)

The Main Idea

Point Charges - __.

2 most commonly used point charges:

1. Protons (e) --> positive point charges, ( q = 1.6e-19 Coulombs)

2. Electrons (-e) --> negative point charges, (q = -1.6e-19 Coulombs)

Like point charges attract, opposite point charges repel. ex. TABLE

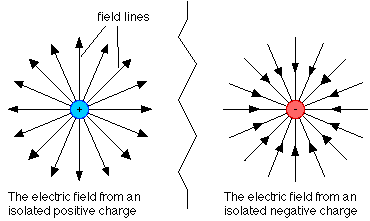
A point charge refers to any particle that has a significantly small radius relative to the distance between it and any observation point of interest. This allows the generalization that all of the particle's charge and mass are localized at a specific point in space. The two known elementary charges are the proton and electron, both of which are modeled as point charges. A single proton holds a charge of +e (1.6e-19C), while an electron holds a charge of -e (-1.6e-19C). Like point charges, such as two positive or two negative charges, repel one another; opposite charges are attracted to one another. This pattern of attraction and repulsion is shown below.

The electric field is an inherent quality of a charged particle. It is defined as a vector field that associates each point in space with the electric force that an infinitesimal test charge would experience. As shown below, the electric field of a positive point charge points radially outward and that of a negative point charge points radially inward. The magnitude of the electric field decreases with increasing distance from the point charge. The source of the electric field in this article is the point charge.

A Mathematical Model

Coulomb Force Law for Point Charges

This law defines the electrical force of attraction or repulsion between two given point charges. The following formula describes the magnitude of this force:

[math]\displaystyle{ \mid\vec F\mid=\frac{1}{4 \pi \epsilon_0 } \frac{\mid Q_1Q_2 \mid}{r^2} }[/math]

[math]\displaystyle{ Q_1, Q_2 }[/math]= The charge of two particles of interest

r = The distance between the two particles

Electric Field due to Point Charge

The Electric Field of a Point Charge can be found by using the following formula:

[math]\displaystyle{ \vec E=\frac{1}{4 \pi \epsilon_0 } \frac{q}{\mid\vec r\mid ^2} \hat r }[/math]

Which is derived from Gauss's Law, modeling the point charge as a sphere.

[math]\displaystyle{ {\epsilon_0} }[/math] is a constant representing vacuum permittivity, the permittivity of free space, or the electric constant, and is approximately [math]\displaystyle{ 8.854*10^{-12}\frac{C^2}{N m^2} }[/math]

[math]\displaystyle{ \frac{1}{4 \pi \epsilon_0 } }[/math] is known as Coulomb's Constant and is approximately [math]\displaystyle{ 8.987*10^{9}\frac{N m^2}{C^2} }[/math]

r is the magnitude of the distance between the observation location and the source location , q is the charge of the particle and [math]\displaystyle{ \hat r }[/math] is the unit vector in the direction of the distance from the source location to the observation point.

Connection Between Electric Field and Force

The force on a given test charge is governed by [math]\displaystyle{ F = Eq }[/math] where E is the electric field and q is the charge of a test charge in Coulombs. This force is represented by Coulomb's Law which was described above.

By solving for the electric field in [math]\displaystyle{ F = Eq }[/math], with F modeled by Coulomb's Law, one obtains the equation for the electric field of the point charge:

[math]\displaystyle{ E = \frac{F}{q_2} = \frac{1}{4 \pi \epsilon_0 } \frac{q_1q_2}{r^2}\frac{1}{q_2}\hat r = \frac{1}{4 \pi \epsilon_0 } \frac{q_1}{r^2} \hat r }[/math]

A Computational Model

Below is a link to a code which can help visualize the Electric Field at various observation locations due to a proton. Notice how the arrows decrease in size by a factor of [math]\displaystyle{ \frac{1}{r^{2}} }[/math] as the observation location gets farther from the proton. The magnitude of the electric field decreases as the distance to the observation location increases.

https://trinket.io/glowscript/725d552305

Two adjacent point charges of opposite sign exhibit an electric field pattern that is characteristic of a dipole. This interaction is displayed in the code below. Notice how the electric field points towards the negatively charged point charge (blue) and away from the positively charged point charge (red).

https://trinket.io/glowscript/f29782cb9d

Examples

Simple

There is an electron at the origin. Calculate the electric field at (4,-3,1)m.

Step 1: Find [math]\displaystyle{ \hat r }[/math]

Find [math]\displaystyle{ \vec r_{obs} - \vec r_{electron} ((4,-3,1) - (0,0,0) = \lt 4,-3,1\gt }[/math]m

Calculate the magnitude of [math]\displaystyle{ \vec r }[/math]. ([math]\displaystyle{ \sqrt{4^2+(-3)^2+1^2}=\sqrt{26} }[/math]

From [math]\displaystyle{ \vec r }[/math], find the unit vector [math]\displaystyle{ \hat{r}. }[/math] [math]\displaystyle{ \lt \frac{4}{\sqrt{26}},\frac{-3}{\sqrt{26}},\frac{1}{\sqrt{26}}\gt }[/math]

Step 2: Find the magnitude of the Electric Field

[math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} = \frac{1}{4 \pi \epsilon_0 } \frac{-1.6 * 10^{-19}}{26} }[/math]

Step 3: Multiply the magnitude of the Electric Field by [math]\displaystyle{ \hat{r} }[/math] to find the Electric Field

[math]\displaystyle{ E = \frac{1}{4 \pi \epsilon_0 } \frac{-1.6 * 10^{-19}}{26}*\lt \frac{4}{\sqrt{26}},\frac{-3}{\sqrt{26}},\frac{1}{\sqrt{26}}\gt = \lt -4.34*10^{-11},3.26*10^{-11},-1.09*10^{-11}\gt N/C }[/math]

Middling

A particle of unknown charge is located at (-0.21, 0.02, 0.11) m. Its electric field at point (-0.02, 0.31, 0.28) m is [math]\displaystyle{ \lt 0.124, 0.188, 0.109\gt }[/math] N/C. Find the magnitude and sign of the particle's charge.

Given both an observation location and a source location, one can find both r and [math]\displaystyle{ \hat{r} }[/math] Given the value of the electric field, one can also find the magnitude of the electric field. Then, using the equation for the magnitude of electric field of a point charge,[math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} }[/math] one can find the magnitude and sign of the charge.

Step 1: Find [math]\displaystyle{ \vec r_{obs} - \vec r_{particle} }[/math].

[math]\displaystyle{ \vec r = (-0.02,0.31,0.28) m - (-0.21,0.02,0.11) m = \lt 0.19,0.29,0.17\gt m }[/math]

To find [math]\displaystyle{ \vec r_{mag} }[/math], find the magnitude of [math]\displaystyle{ \lt 0.19,0.29,0.17\gt }[/math]

[math]\displaystyle{ \sqrt{0.19^2+0.29^2+0.17^2}=\sqrt{0.1491}= 0.39 }[/math]

Step 2: Find the magnitude of the Electric Field

[math]\displaystyle{ E= \lt 0.124, 0.188, 0.109\gt N/C }[/math]

[math]\displaystyle{ E_{mag} = (\sqrt{0.124^2+0.188^2+0.109^2}=\sqrt{0.0626}=0.25 }[/math]

Step 3: Find q by rearranging the equation for [math]\displaystyle{ E_{mag} }[/math]

[math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} }[/math]

By rearranging this equation we get

[math]\displaystyle{ q= {4 pi * epsilon_0 } *{r^2}*E_{mag} }[/math]

[math]\displaystyle{ q= {1/(9*10^9)} *{0.39^2}*0.25 }[/math]

[math]\displaystyle{ q= + 4.3*10^{-12} C }[/math]

Difficult

The electric force on a -2mC particle at a location (3.98 , 3.98 , 3.98) m due to a particle at the origin is [math]\displaystyle{ \lt -5.5*10^{3} , -5.5*10^{3}, -5.5*10^{3}\gt }[/math] N. What is the charge on the particle at the origin?

Given the force and charge on the particle, one can calculate the surrounding electric field. With this variable found, this problem becomes much like the last one.

[math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r_{mag}^2} }[/math]

to find the rmag value. To find [math]\displaystyle{ \hat r }[/math] we can find the direction of the electric field as that is obviously going to be in the same direction as [math]\displaystyle{ \hat r }[/math]. Then, once we find [math]\displaystyle{ \hat r }[/math], all that is left to do is multiply [math]\displaystyle{ \hat r }[/math] by rmag and that will give us the [math]\displaystyle{ r }[/math] vector. We can then find the location of the particle as we know [math]\displaystyle{ r=r_{observation}-r_{particle} }[/math]

Step 1: Find the magnitude of the Electric field.

[math]\displaystyle{ F = Eq }[/math]

[math]\displaystyle{ \lt 5.5*10^{3}, -7.6*10^{3}, 0\gt = E * -2mC }[/math]

[math]\displaystyle{ E = \frac{\lt -5.5*10^{3} , -5.5*10^{3}, -5.5*10^{3}\gt }{-2mC} = \lt 2.75*10^{6} , 2.75*10^{6} , 2.75*10^{6}\gt }[/math] N/C

Step 2:: Find [math]\displaystyle{ \vec r_{obs} - \vec r_{particle} }[/math].

[math]\displaystyle{ \vec r = (3.98 , 3.98 , 3.98) m - (0 , 0 , 0) m = \lt 3.98 , 3.98 , 3.98\gt m }[/math]

To find [math]\displaystyle{ \vec r_{mag} }[/math], find the magnitude of [math]\displaystyle{ \lt 3.98 , 3.98 , 3.98\gt }[/math]

[math]\displaystyle{ \sqrt{3.98^2+3.98^2+3.98^2}=\sqrt{47.52}= 6.9 }[/math]

Step 3: Find the magnitude of the Electric Field

[math]\displaystyle{ E= \lt 2.75*10^{6} , 2.75*10^{6} , 2.75*10^{6}\gt }[/math] N/C

[math]\displaystyle{ E_{mag} = (\sqrt{(2.75*10^{6})^2+2.75*10^{6})^2+2.75*10^{6})^2}=\sqrt{2.27*10^{13}}=4.76*10^{6} }[/math]

Step 4: Find q by rearranging the equation for [math]\displaystyle{ E_{mag} }[/math]

[math]\displaystyle{ E_{mag}= \frac{1}{4 \pi \epsilon_0 } \frac{q}{r^2} }[/math]

By rearranging this equation we get

[math]\displaystyle{ q= {4 pi * epsilon_0 } *{r^2}*E_{mag} }[/math]

[math]\displaystyle{ q= {1/(9*10^9)} *{6.9^{2}}*4.76*10^{6} }[/math]

[math]\displaystyle{ q= + 0.253 C }[/math]

Connectedness

1.How is this topic connected to something that you are interested in?

The electric field of a single point charge is the most basic application of the fundamental property. It is the combined electric field that results from many point charges packed in the same region that causes atomic level changes such as polarization. I am interested in the topic of polarization because it is what directs the movement of current through conductors.

2.How is it connected to your major?

As a BME major, I learn to work with many types of electronics that involve circuits, capacitors, and resistors, to build medical devices. The movement of current through these electronics is dependent on the presence of an electric force (caused by the electric field) on a negatively charged point charge. Specifically, my BMED 2250 group is currently designing a device that includes a capacitive touch sensor. This sensor works due to the charge transfer between two charged plates of a capacitor. The charge transfer is driven by the attraction of oppositely charged point charges and their corresponding electric fields.

3.Is there an interesting industrial application?

Electric fields are actually used in tissue engineering to determine the properties of cells and tissues. They are also used in electrokinetics to assemble artificial tissues from cells.

History

Charles de Coulomb

Charles de Coulomb was born in June 14, 1736 in central France. He spent much of his early life in the military and was placed in regions throughout the world. He only began to do scientific experiments out of curiously on his military expeditions. However, when controversy arrived with him and the French bureaucracy coupled with the French Revolution, Coulomb had to leave France and thus really began his scientific career.

Between 1785 and 1791, de Coulomb wrote several key papers centered around multiple relations of electricity and magnetism. This helped him develop the principle known as Coulomb's Law, which confirmed that the force between two electrical charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them. This is the same relationship that is seen in the electric field equation of a point charge.

Retrieved November 28, 2016, from http://www.biography.com/people/charles-de-coulomb-9259075#controversy-and-absolution

@@ Line 6: / Line 6: @@
 '''Point Charges''' - __.
-most commonly used point charges:
+<u> 2 most commonly used point charges: </u>
 . Protons (e) --> positive point charges, ( q = 1.6e-19 Coulombs)
 . Electrons (-e) --> negative point charges, (q = -1.6e-19 Coulombs)
 ''Like'' point charges ''attract'', ''opposite'' point charges ''repel''.