Energy graphs and the Bohr model: Difference between revisions
(inserted photo and source) |
(covers quantum states.) |
||
| Line 51: | Line 51: | ||
[[File:colorbohr3.jpg]] | [[File:colorbohr3.jpg]] | ||
Hydrogen specifically gives of | Hydrogen specifically gives of light waves with the wavelengths that correspond to red, glue green, and violet. | ||
==Connectedness== | ==Connectedness== | ||
| Line 64: | Line 64: | ||
A more complete history can be found on the main Bohr Model page. | A more complete history can be found on the main Bohr Model page. | ||
== Spectral Lines of Hydrogen Application== | ==Spectral Lines of Hydrogen Application== | ||
[[File:Spectral_hydrogen.png|200px|thumb|left|spectral hydrogen transition for hydrogen atoms]] | |||
[5] | [5] | ||
The Bohr model explains the energy levels of electrons. Atoms all have electrons that orbit the nucleus and there exists an electromagnetic force between the protons and electrons. This force contains energy and causes the atom to experience a set of quantum states. These quantum states. See below '''quantum states'''. The Bohr model visualizes the quantum states. It labels it based on the electron’s principal number (from the quantum states). Spectral emission happens when an electron moves from a quantum state with more energy to one with less energy. The difference between the initial and final state corresponds to the emitted photon (which gives us visual evidence of the transition). This emitted light corresponds to a certain spectral series. See also [[spectral series]]. | |||
=='''Quantum states'''== | |||
Each of the quantum states listed below helps to describe the characteristics of a specific electron (shell, shape, path, and spin). This gives us a better understanding of the attributes of that electron so that we can have a better understanding of the atom by analyzing the parts that make up the system. The electrons of an atom can be described using 4 quantum numbers (n, ℓ, mℓ, s). Together, all of these numbers create a unique quantum state that describes the electron in question. Each electron has a specific quantum number. Below we will proceed to define each quantum number. | |||
== Principal quantum number (n) == | |||
This describes the shell that the atom is housed in. this value (n) starts at 1 and goes until you hit the outermost valence electron shell. | |||
== Azimuthal quantum number (ℓ) == | |||
[[File:Azimuthal.png|200px|thumb|left|azimuthal formula]] | |||
This is also called the angular momentum quantum number or orbital quantum number and describes the orbital angular momentum within the subshell. This is also where s,p,d, and f orbitals are relevant because those represent the ℓ in the equation. For this it ranges from 0 to n-1 because the “s” subshell counts as 0 and it moves up from there. Based on the angular momentum, it decides the shape of the orbital. The chart below should help clear some things up. | |||
[[File:Azimuthal p2.png|200px|thumb|left|clarifying azimuthal states chart]] | |||
[6] | |||
== Magnetic quantum number (mℓ) == | |||
The quantum number describes the specific orbital cloud that the electron inhabits. This analyzes the projected angular momentum along a certain axis using orbitals we learned from the azimuthal quantum number. Ultimately it tells you the orientation of the orbital using the angular momentum so that you can know how the electron travels along the path within the subshell. By using the angular momentum, we can know how fast and in what direction the electron is going within the designated subshell. | |||
[[File:Magnetic electorn.png|200px|thumb|left|magnetic electron number formula]] | |||
== Spin quantum number (s) == | |||
This describes the spin of the angular momentum (from the magnetic quantum number) to further describe the path of the electron. This is either -½ (for an electron spinning down) or ½ (for an electron spinning upwards). | |||
Together, using the principle, azimuthal, magnetic quantum, and spin quantum numbers, we can describe the full characteristics of an electron. These all form a unique quantum state for each electron that helps determine the electromagnetic force between the protons and electron as well as the overall energy of an atom. The Bohr model helps to visualize the quantum states of a hydrogen atom and uses a shell labeling system (literally corresponding with the principle number from our quantum states). | |||
== See also == | == See also == | ||
| Line 88: | Line 125: | ||
5. https://courses.lumenlearning.com/cheminter/chapter/spectral-lines-of-hydrogen/ | 5. https://courses.lumenlearning.com/cheminter/chapter/spectral-lines-of-hydrogen/ | ||
6. https://en.wikipedia.org/wiki/Azimuthal_quantum_number#:~:text=The%20azimuthal%20quantum%20number%20is,the%20shape%20of%20the%20orbital. | |||
[[Category:Energy]] | [[Category:Energy]] | ||
Revision as of 22:42, 28 November 2021
Allison Fain Fall 2021
The Main Idea
Energy graphs and the Bohr model.
This page gives a more in-depth explanation of how to use energy graphs to comprehend the Bohr model. It specifically explains how to illustrate the various aspects such as excited states and photon emissions or absorptions on the energy graphs as well as what each component corresponds to.
A Mathematical Model
The Bohr Model, as explained in more detail on the Bohr Model wiki, page depicts the atom as a small, positively charged nucleus surrounded by electrons which can only be at certain different distances from the proton to which it is bound. Energy is quantized which means that only orbits with certain radii are allowed.[1] These levels are labeled with integer N, known as quantum number, where the lowest energy state is the ground state. Beyond an energy called the ionization potential the single electron of the hydrogen atom is no longer bound to the atom. The Bohr model works well for very simple atoms such as hydrogen.
Electronic Energy levels of a Hydrogen Atom
E = K + Uelectric
1) [math]\displaystyle{ E = {\frac{mv^2}{2}} - {\frac{{\frac{1}{2}}*{\frac{1}{4π ε0}}*{\frac{me^2}{h*}}}{N^2}} }[/math]
2) [math]\displaystyle{ E = {\frac{13.6 eV}{N^2}} }[/math] where N = 1,2,3
A Computational Model
Visualize this topic given this glow script written by matter and interactions Bohr Model Glowscript [3]
Examples
Simple
This Bohr model picture helps you visualize the orbit radii of the different excited states of the hydrogen atom described in the Bohr model. It displays how the distances in orbit radii get increasingly larger. This also means that due to the fact that the distance from the center is much larger, the ionization energy is much less. [2] The Bohr model shows us that electron orbits aren't equally spaced and that as you get farther from the nucleus (as your get more energy), the spacing between these levels decreases.
This visualization of the orbitals in a more graphical way shows that as the distance from the center becomes larger, the ionization energy is much less. [2]
Middling
This graph explains in more detail how each level corresponds to less energy. If the energy reached zero, the electron would be free from the hydrogen nucleus because no energy is holding it on. The levels get exponentially closer as they approach the ionization energy
Difficult
When energy is added, the electron moves up to the next orbital. This is called atomic excitation. This energy is released as a photon (light energy) and the electron moves back down.
Hydrogen specifically gives of light waves with the wavelengths that correspond to red, glue green, and violet.
Connectedness
Though it is not related to my major, one of my favorite classes I took at Georgia Tech was Earth and Atmospheric Sciences. I found it immensely fascinating when I realized that the same ideology is used as described here as is used to determine the composition of things in space. These emission spectra can be utilized to determine the type of elements that are in stars. Without this method, we would not know what stars are composed of. The ability to study the emission spectra gives us the capabilities to understand where stars come from as well as ideas of the origins of our universe. [4]
History
Ernest Rutherford created the Rutherford Model in 1911 which consisted of a planetary-model atom. His model had flaws including the fact that he thought the electron would lose energy gradually causing it to spiral inwards. However, in 1913 Niehls Bohr proposed the Bohr Model which suggested new ideas regarding the motion of electrons. These new ideas fixed the flaws in the Rutherford Model but are oversimplifications of reality. In 1925, a more accurate model of electron motion was proposed by Werner Heisenberg called quantum mechanics. Today, the Bohr model is taught as a simplified way to understand the mechanics of electrons and can be used fairly accurately in simply elements such as hydrogen, consisting of one single electron. A more complete history can be found on the main Bohr Model page.
Spectral Lines of Hydrogen Application

[5]
The Bohr model explains the energy levels of electrons. Atoms all have electrons that orbit the nucleus and there exists an electromagnetic force between the protons and electrons. This force contains energy and causes the atom to experience a set of quantum states. These quantum states. See below quantum states. The Bohr model visualizes the quantum states. It labels it based on the electron’s principal number (from the quantum states). Spectral emission happens when an electron moves from a quantum state with more energy to one with less energy. The difference between the initial and final state corresponds to the emitted photon (which gives us visual evidence of the transition). This emitted light corresponds to a certain spectral series. See also spectral series.
Quantum states
Each of the quantum states listed below helps to describe the characteristics of a specific electron (shell, shape, path, and spin). This gives us a better understanding of the attributes of that electron so that we can have a better understanding of the atom by analyzing the parts that make up the system. The electrons of an atom can be described using 4 quantum numbers (n, ℓ, mℓ, s). Together, all of these numbers create a unique quantum state that describes the electron in question. Each electron has a specific quantum number. Below we will proceed to define each quantum number.
Principal quantum number (n)
This describes the shell that the atom is housed in. this value (n) starts at 1 and goes until you hit the outermost valence electron shell.
Azimuthal quantum number (ℓ)
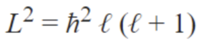
This is also called the angular momentum quantum number or orbital quantum number and describes the orbital angular momentum within the subshell. This is also where s,p,d, and f orbitals are relevant because those represent the ℓ in the equation. For this it ranges from 0 to n-1 because the “s” subshell counts as 0 and it moves up from there. Based on the angular momentum, it decides the shape of the orbital. The chart below should help clear some things up.

[6]
Magnetic quantum number (mℓ)
The quantum number describes the specific orbital cloud that the electron inhabits. This analyzes the projected angular momentum along a certain axis using orbitals we learned from the azimuthal quantum number. Ultimately it tells you the orientation of the orbital using the angular momentum so that you can know how the electron travels along the path within the subshell. By using the angular momentum, we can know how fast and in what direction the electron is going within the designated subshell.
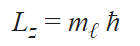
Spin quantum number (s)
This describes the spin of the angular momentum (from the magnetic quantum number) to further describe the path of the electron. This is either -½ (for an electron spinning down) or ½ (for an electron spinning upwards).
Together, using the principle, azimuthal, magnetic quantum, and spin quantum numbers, we can describe the full characteristics of an electron. These all form a unique quantum state for each electron that helps determine the electromagnetic force between the protons and electron as well as the overall energy of an atom. The Bohr model helps to visualize the quantum states of a hydrogen atom and uses a shell labeling system (literally corresponding with the principle number from our quantum states).
See also
Bohr Model Main Page
External links
[1][1]
References
1. http://csep10.phys.utk.edu/astr162/lect/light/bohr.html
2. http://hyperphysics.phy-astr.gsu.edu/hbase/hyde.html
4. http://skyserver.sdss.org/dr1/en/proj/advanced/spectraltypes/lines.asp
5. https://courses.lumenlearning.com/cheminter/chapter/spectral-lines-of-hydrogen/




