Quantum Properties of Light

Giovanny Espitia, Spring 2022

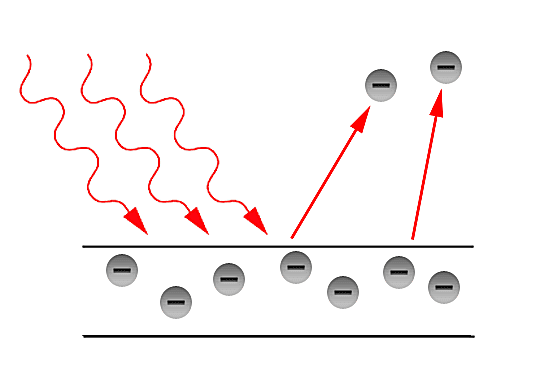
Why do we need a quantum interpretation?

In the latter part of the 19th century, the classical description of light that had prevailed since the 17th century, began to fail in its explanatory power for the ever more precise measurements and phenomena being performed and observed in laboratories. The prime example of such failure is the so - called Ultraviolet Catastrophe. This term was first used by Paul Ehrenfest to refer to Rayleigh - Jeans law ability to predict experimental results below energies of [math]\displaystyle{ 10^{5} }[/math] and its sudden unexplained divergence at energies close to the ultraviolet range in the electromagnetic spectrum. Such discrepancies called for a more fundamental description of light. Fortunately, in the year 1900, Max Planck through his introduction of an ad - hoc assumption, was able to correctly explained the Black - body radiation problem. Planck later referred to such ad - hoc assumption as an "act of desperation". Moreover, in 1905, Einstein further validated the assumption made by Planck in his solution for the Black - body problem. The assumption was to treat light as if it came in discrete - packets later referred to as "Quanta". With such assumption, Einstein made further progress in explaining past experiments such as the Photoelectric effect first observed by Hertz in the latter part of the 19th century.

The Main Idea

Einstein, Planck, and Compton showed the explanatory power of giving light a discrete or quantum interpretation. In his theory of the photoelectric effect, Einstein showed that the energy [math]\displaystyle{ E }[/math] of a photon is simply the product [math]\displaystyle{ h\nu }[/math], where [math]\displaystyle{ h }[/math] is Planck’s constant and [math]\displaystyle{ \nu }[/math] is the frequency of the photon. As mentioned before, such treatment was allowed for the understanding of problems such as the Black - body, the Photoelectrons, and the scattering of electrons upon the contact of high energy electromagnetic radiation and light.

Mathematical Model

The energy of a photon

[math]\displaystyle{ E = h\nu }[/math]

Where:

1. [math]\displaystyle{ h = 6.626*10^{-34} }[/math]
2. [math]\displaystyle{ \nu = \frac{c}{\lambda} }[/math]

Here, [math]\displaystyle{ c }[/math] is the speed of light and [math]\displaystyle{ \lambda }[/math] is the wavelength of the photon.

Frequency - Wavelength Relationship:

[math]\displaystyle{ c = \lambda\nu }[/math]

Linear momentum of a photon

In the classical perspective, a photon should not carry any momentum since it is a massless boson. However, Einstein showed us through the following relationship that the former statement is not true.

[math]\displaystyle{ E = cp }[/math]

Where [math]\displaystyle{ c }[/math] is the speed of light and [math]\displaystyle{ p }[/math] is the momentum of the photon.

Therefore and according to the energy of a photon expression introduced in the previous subsection

[math]\displaystyle{ E = h\nu = cp }[/math]

Solving for [math]\displaystyle{ p }[/math],

[math]\displaystyle{ p = \frac{h\nu}{c} }[/math]

Interestingly, if we rearrange the above expression in terms of wavelength, we arrive at the same result as De Broglie for the wavelength of a matter wave. This is done as follows:

[math]\displaystyle{ p = \frac{h\nu}{c} }[/math]

Using the frequency - wavelength relationship introduced in a previous section, we make the appropriate substitution. Namely,

[math]\displaystyle{ p = \frac{h\nu}{c} = \frac{h}{\lambda} }[/math]

The last step, is simply to solve for [math]\displaystyle{ \lambda }[/math]. This step is left as an exercise to the reader.

Pair Production

When a photon has energy in the gamma - ray region of the electromagnetic spectrum and is close to an atomic nucleus, the product of such interaction often results in an electron - positron pair. A positron is the electron’s analog in antimatter. In other words, both have equal mass but a differing charge. This is often expressed as follows:

[math]\displaystyle{ \gamma \rightarrow e^{-} + e^{+} }[/math]

Where [math]\displaystyle{ \lambda }[/math] is the symbol for the photon and [math]\displaystyle{ e^{-}, e^{+} }[/math] are the symbols for the electron and positron, respectively. In order for pair - production to occur, the photon’s energy, [math]\displaystyle{ h\nu }[/math] must be larger than the rest mass energy, [math]\displaystyle{ 2m_{e}c^{2} }[/math], of the two particles.

Connectedness

This relation allows us to understand the photoelectric effect (why some metals emit electrons when light is shined on them) and Planck's Law of Black Body Radiation.

Every day in the biomedical device industry, new forms of treatment for cancer are being used. Proton emission therapy is a current method. If photons were ever used to combat disease, Planck's Relation could help engineers to calculate their energy or radiation frequency and wavelength in order to adjust these values to get the ones desired.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

HyperPhysics page on Photoelectric Effect: http://hyperphysics.phy-astr.gsu.edu/hbase/mod2.html#c3

External links

A thorough example of a problem calculating the energy in a mole of photons using Planck's Relation: [1]

References

http://hyperphysics.phy-astr.gsu.edu/hbase/mod2.html#c3 https://www.youtube.com/watch?v=dSUvyERhtO8