Magnetic Force in a Moving Reference Frame: Difference between revisions

Revision as of 21:39, 24 April 2022

This page is claimed by Paul Vollrath Spring 2022

The Main Idea

The magnetic force of a moving charge depends on the velocity of the charge, and thus can differ according to different moving reference frames.

Magnetic fields were initially formalized under Maxwell's framework in 1865 given by the following equations known as Maxwell's Equations;

[math]\displaystyle{ \nabla \cdot \textbf{E} = \rho }[/math]

[math]\displaystyle{ \nabla \cdot \textbf{B} = 0 }[/math]

[math]\displaystyle{ \nabla \times \textbf{E} = -\frac{\partial\textbf{B}}{\partial t} }[/math]

[math]\displaystyle{ \nabla \times \textbf{B} = \mu_{0}\textbf{j} + \mu_{0}\epsilon{0}\frac{\partial\textbf{E}}{\partial t} }[/math]

These equations have remained remarkably robust in the face of more recent discoveries in physics such as Einstein's theories of special and general relativity, as well as quantum mechanics. However, limited as Maxwell was by the knowledge and technology of his time, magnetism is more formally derived from special relativity in most modern textbooks.

Take two electrons, [math]\displaystyle{ e_{1} }[/math] and [math]\displaystyle{ e_{2} }[/math], traveling parallel to one another with the same velocity, as seen from a stationary observer. The equation for the magnetic force between these two electrons is zero from the more classical definition of magnetism, since the relative motion of these charges is zero;

[math]\displaystyle{ \textbf{F}=q\vec{v} \times \textbf{B} }[/math]

However, with Einstein's special theory of relativity, the understanding of this system is altered since from the reference point of either electron, the velocity of the other electron is dilated to account for its motion through space - dilated by the gamma factor;

[math]\displaystyle{ \gamma = \sqrt{\frac{1}{1-\frac{v^2}{c^2}}} }[/math]

According to the Special Theory of Relativity, distance and time are dilated as a result of relative motion, and is dependent on the reference frame from which observations are made. Since from the reference frame of each electron, the velocity of the other electron is dilated by the \gamma factor, from the reference frame of an electron, the other electron is no longer traveling at the same velocity. Hence, now there is relative motion between these two electrons, and there is a magnetic force between these two particles.

Note: the derivation of electromagnetism from special relativity is presented more formally here - [1]

A Mathematical Model

Let's consider two moving protons to simplify the case. Suppose the two protons are initially traveling parallel to each other with the the same speed. The speed is v, and the two particles are distance, r, apart.

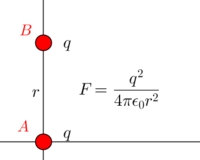
Two protons, distance r apart, moving parallel with velocity, v

How would we find the electric and magnetic force that the top proton exerts on the bottom?

First: Electric force is easily calculated by calculating the electric field, [math]\displaystyle{ {\vec{E}_{top}} }[/math], at the location of proton[math]\displaystyle{ _{bottom} }[/math]. The equation for electric force is [math]\displaystyle{ {\vec{F}_{E, bottom}} = q_{bottom}{\vec{E}_{top}} }[/math]. Therefore: [math]\displaystyle{ {\vec{F}_{E, bottom}} = {\frac{1}{4πϵ_0}}{\frac{e^{2}}{r^{2}}} }[/math].

Second: Determine magnetic field. [math]\displaystyle{ {\vec{F}_{M, bottom}} }[/math] by calculating the magnetic field [math]\displaystyle{ {\vec{B}_{top}} }[/math]. [math]\displaystyle{ {\vec{B}_{top}} = {\frac{\mu_{0}}{4\pi}} }[/math] [math]\displaystyle{ {\frac{q_{top}{\vec{v}_{top}}{\times}{\hat{r}}}{r^{2}}} }[/math]. Using this equation and right hand rule, we can see that the magnetic field goes into the page at the location of proton 2. Additionally [math]\displaystyle{ {\vec{v}_{top}}{\times}{\hat{r}} }[/math] can be rewritten as sin(90), which equals +1.

Three: The magnetic field from the previous step can be used to determine the magnetic force on the bottom proton. [math]\displaystyle{ {\vec{F}_{M, bottom}} = q_{bottom}{\vec{v}_{bottom}}{\times}{\vec{B}_{top}} }[/math].

The magnetic force is found to be upward and can be found with the equation: [math]\displaystyle{ {\vec{F}_{M, bottom}} = {\frac{\mu_{0}}{4\pi}} }[/math] [math]\displaystyle{ {\frac{e^{2}v^{2}}{r^{2}}} }[/math].

Magnetic force and Electric force on two parallel protons

When we take the ratio of the magnetic force to the electric force, we find that the forces have relations to the speed of light. When particles move at ordinary speed the magnetic interaction is insignificant when compared to the electric interaction. However, if the speed reaches the speed of light the magnetic force comes to par with the electric force.

A Computational Model

Magnetic force is easy to visualize because it takes only the speed and magnetic field with the right hand rule to calculate. However, the easiest way to visualize magnetic force in moving reference points is to imagine a car driving past and then imagine a car driving along side you. In the first case the car is the object that is moving. However, in the second case because the reference frame is moving alongside the observed object there is no change (if going the exact same speed).

Computationally, determining magnetic field strength with reference to moving reference frames, to say determine the force due to a magnetic field on a particle moving in that reference frame, is very simple. The following code is written in python and makes use of python's Numpy module to calculate a simple cross product of a particle's velocity, after accounting for a change in reference frame. The code is shown below.

    import numpy as np

    partVel = np.array([3,5,7],float)
    magStrenght = np.array([0,0,1],float)
    qCharge = 1

    print("Input reference frame velocity relative to stationary reference frame (V_x,V_y,V_z)")
    xRef = input("V_x = ")
    yRef = input("V_y = ")
    zRef = input("V_z = ")
    refVel = np.array([xRef,yRef,zRef],float)

    def magneticForce(velocity):
        velocity -= refVel
        return qCharge * np.cross(velocity,magStrength)

    print(magneticForce(partVel))

This code does not make any relativistic adjustments for velocity, as it assumes a particle is moving much slower than the speed of light. However, relativistic adjustments can be made simply by including a [math]\displaystyle{ \gamma }[/math] term when calculating the velocity of the moving particle in the new reference frame. Since as a vector sum of two velocities (as is the case when switching reference frame) in relativistic cases can be represented by the following;

[math]\displaystyle{ \vec{v} + \vec{u} = \frac{\vec{v} + \vec{u}}{1 - \frac{\vec{v}\vec{u}}{c^2}} }[/math]

Adding the code snipped below adjusts the prior code to make relativistic adjustments - Noting that the effects of special relativity are always present, but insignificant when the velocities are much lower than the speed of light. The reason for this is that the value of gamma is almost exactly 1 until the particle's velocity approaches the speed of light, at which point it asymptotically goes to infinity at the speed of light. A graph of the value of gamma as a function of velocity is shown below.

    newVel = (partVel + refVel)/(1 - (partVel*refVel)/c**2)

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Gamma as a function of Velocity

Note: Linked code does not run in the Wiki page, but can be copy pasted into another code IDE and run without issue. Code returns the force on a particle moving in a constant magnetic field adjusted to be measured with reference to an inputed reference frame.

File:/Desktop/code.jpg

Simulated image of magnetic field lines

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

A proton travels in the x-direction, with speed 1E5 m/s. At the location of the proton there is a magnetic field of 0.25T in the y-direction, because of a coil. What are the direction and magnitude of the magnetic force on the proton?

Step 1: The magnetic force can be calculated by using: [math]\displaystyle{ {\vec{F}} = q({\vec{v}}{\times}{\vec{B}}) }[/math]

q - charge of proton (1.6E-19 C)

[math]\displaystyle{ {\vec{v}} }[/math] - velocity

[math]\displaystyle{ {\vec{B}} }[/math] - magnetic field

Step 2: Plug in values into the equation to find the magnetic force.

[math]\displaystyle{ {\vec{v}}{\times}{\vec{B}} = [(1e5 m/s){\times}(0.25)][(\hat{i}){\times}(\hat{j})] = 2.5e4 mT/s (\hat{k}) }[/math]

[math]\displaystyle{ {\vec{F}} = (1.6e-19 C){\times}(2.5e4 mT/s) = 4e-15 N }[/math]

Middling

An electron moves with speed v, in a region with uniform magnetic field B into the page due to large cols. Draw the trajectory of the electron.

Step 1: Apply magnetic force equation.

[math]\displaystyle{ {\vec{F}} = -evB{\sin{90}} }[/math]

Step 2: Draw the trajectory of the electron.

Difficult

A long solenoid with diameter of 4cm is in a vacuum and a lithium nucleous is in a clockwise circular orbit inside the solenoid. It takes 50ns for the lithium nucleus to complete one orbit

(a) Does the current in the solenoid run clockwise or counterclockwise? Explain.

The current in the solenoid in the lithium is clockwise and solenoid. You just never ran my products officially.

(b) What is the magnitude of the magnetic field made by the solenoid?

Q = 3p = 3*1.6*10^19 =7m_{p} [math]\displaystyle{ {\vec{F}_B} = {QvB} QvB = mv^2/R B = mv/QR }[/math]

[math]\displaystyle{ {\frac{v}{R}} = \frac{2\pi}{t} }[/math]

Side view of solenoid with current and magnetic field

[math]\displaystyle{ B = m {\frac{2\pi}{Qt}} }[/math] =(7x1.67e-27)(2pi/(50e-9)(3x1.6e-19) = 3.05 T

Connectedness

How is this topic connected to something that you are interested in? This topic is interesting because it can be confusing exactly what causes a magnetic force when both the object in question and the reference frame is in motion. The changes in magnetic and electric field due to a change in the reference frame is interesting to note.
How is it connected to your major? As a BME it is important to be able to understand the consequences or benefits of looking at a phenomenon in a different angle. However, it is important to note that there is only one force resulting from the magnetic and electric fields. Additionally, magnetic forces would be beneficial when dealing with development of devices including current-carrying wires.
Is there an interesting industrial application? Magnetic forces on current-carrying wires are usually larger than the electric force on the same wire, because the net charge is zero. Moreover, when the speed of the particle is less than the speed of light there is less magnetic interaction between 2 charged particles. When the speed exceeds the speed of light, magnetic force between two charged particles can be compared to the electric force.

History

In 20th century, relativity and quantum mechanics were brought into light. In 1905, Albert Einstein published a paper which proved that electric and magnetic fields both take part in the same phenomenon when viewed from different referenced frames.[2] Einstein developed his theory of relativity through a simple experiment of a moving magnet and a conductor. In this experiment, the current in the conductor is calculated in the frame of reference of both the magnet and the conductor. [3] According to the basic principle of relativity the only known variable, current, is unchanging in both reference frames. However, when Maxwell's Equations are applied there is a magnetic force in the magnet frame and an electric force in the conductor frame. This thought experiment as well as Fizeau experiment, the aberration of light, and negative aether drift tests formed the foundation for the theory of relativity.[4] With a new found understanding of relativity, quantum mechanics combined with electrodynamics to create a new science called quantum electrodynamics (QED). Simply put, QED describes the interaction between light and matter. Additionally, it is the first theory where there is no discord between quantum mechanics and special relativity.[5]

External links

Michigan State University: Moving Reference Frames[7]

University of Melbourne: Why do Magnetic Forces Depend on Who Measures Them?[8]

References

@@ Line 85: / Line 85: @@
 <math> \vec{v} + \vec{u} = \frac{\vec{v} + \vec{u}}{1 - \frac{\vec{v}\vec{u}}{c^2}} </math>
-Adding the code snipped below adjusts the prior code to make relativistic adjustments - Noting that the effects of special relativity are always present, but insignificant when the velocities are much lower than the speed of light.
+Adding the code snipped below adjusts the prior code to make relativistic adjustments - Noting that the effects of special relativity are always present, but insignificant when the velocities are much lower than the speed of light. The reason for this is that the value of gamma is almost exactly 1 until the particle's velocity approaches the speed of light, at which point it asymptotically goes to infinity at the speed of light. A graph of the value of gamma as a function of velocity is shown below.
       newVel = (partVel + refVel)/(1 - (partVel*refVel)/c**2)
+[[File:gammaFunc.png|thumb|Gamma as a function of Velocity]]
 ''Note: Linked code does not run in the Wiki page, but can be copy pasted into another code IDE and run without issue. Code returns the force on a particle moving in a constant magnetic field adjusted to be measured with reference to an inputed reference frame.''