Spontaneous Photon Emission: Difference between revisions
Delaney.mcg (talk | contribs) |
Delaney.mcg (talk | contribs) No edit summary |
||
| Line 11: | Line 11: | ||
In accordance with the law of conservation of energy, if we chose a system that includes both the photon and the atom, this process will feature no net energy change. | In accordance with the law of conservation of energy, if we chose a system that includes both the photon and the atom, this process will feature no net energy change. | ||
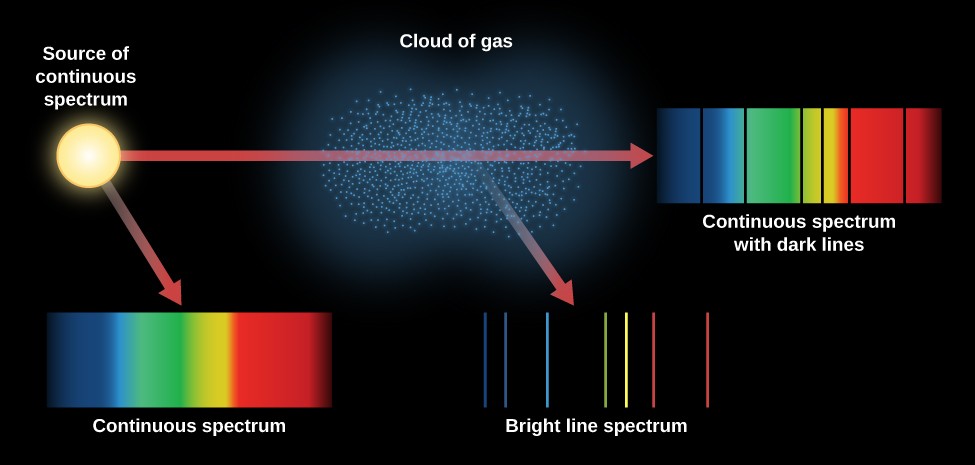
The collection of photon emissions for an atom's transition from a higher to a lower state is called an emission spectrum. For any given atom in an excited state, there typically exists a wide range of potential photon emissions, and these emissions vary greatly between different elements. The capture of these photon emission patterns with diffraction gradient apparatuses is call spectroscopy. Spectroscopy is used heavily in fields like astronomy to determine the chemical composition of light sources too distant to observe directly. | The collection of photon emissions for an atom's transition from a higher to a lower state is called an emission spectrum. For any given atom in an excited state, there typically exists a wide range of potential photon emissions, and these emissions vary greatly between different elements. The capture of these photon emission patterns with diffraction gradient apparatuses is call spectroscopy. | ||
Spectroscopy is used heavily in fields like astronomy to determine the chemical composition of light sources too distant to observe directly. | |||
[[File: astronomy_spectral_lines.jpg]] | |||
[[File:HEM.png]] | [[File:HEM.png]] | ||
[[File:Krypton Spectrum.jpg]] | [[File:Krypton Spectrum.jpg]] | ||
Above you'll see the emissions spectrums for hydrogen and krypton respectively. As you can see, krypton has a much wider range of potential photon emissions, largely because its atoms are far more complex than those of a more simple element like hydrogen. | Above you'll see the emissions spectrums for hydrogen and krypton respectively. As you can see, krypton has a much wider range of potential photon emissions, largely because its atoms are far more complex than those of a more simple element like hydrogen. | ||
Revision as of 11:32, 29 April 2022
Claimed by Delaney McGowan Spring 2022
Spontaneous photon emission is a quantum effect that occurs when an atom or other quantum system decreases its energy level and releases a photon in a random direction. This process is referred to as spontaneous because the atoms decrease in energy level is caused by a loss of energy that occurs simply due to time. This process should not be confused with stimulated photon emission, a process that must be incited with the absorption of other particles. This release of a photon results in the production of light, referred to as luminescence. Luminescence has been instrumental in many inventions, such as fluorescent lights, television displays and light emitting diodes. Most notable, lasers use spontaneous photon emission to start up, and stimulated photon emission to continue running.
The Main Idea
Spontaneous photon emission is a great example of the need for quantum theory. Because electron states used to characterize atoms are formally considered stationary states (time independent), we must find an explanation for why this time dependent behavior occurs. Quantum behavior explains this by taking into account the interactions of photons and electrons, in where the initial state of an atomic electron is just an electron but the final state of the system can be an electron and proton. There are currently no quantum models to describe this, but because of our current understanding of quantum theory, we know it does not violate our currently understanding of quantum behavior.
If an atom is in an excited state, its current energy level is higher than the minimum energy level, or ground state (n=1). In this state, it is possible for it to undergo the process of spontaneous photon emission, decreasing its energy level to one closer to the ground state (n-1). During this process, the atom will emit a photon with energy equal to the difference in energy between its starting and ending energy levels.
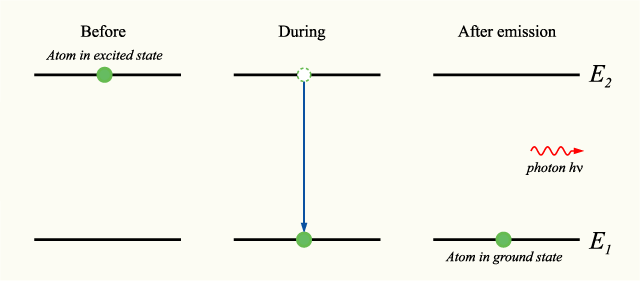
In accordance with the law of conservation of energy, if we chose a system that includes both the photon and the atom, this process will feature no net energy change. The collection of photon emissions for an atom's transition from a higher to a lower state is called an emission spectrum. For any given atom in an excited state, there typically exists a wide range of potential photon emissions, and these emissions vary greatly between different elements. The capture of these photon emission patterns with diffraction gradient apparatuses is call spectroscopy.
Spectroscopy is used heavily in fields like astronomy to determine the chemical composition of light sources too distant to observe directly.

 Above you'll see the emissions spectrums for hydrogen and krypton respectively. As you can see, krypton has a much wider range of potential photon emissions, largely because its atoms are far more complex than those of a more simple element like hydrogen.
Above you'll see the emissions spectrums for hydrogen and krypton respectively. As you can see, krypton has a much wider range of potential photon emissions, largely because its atoms are far more complex than those of a more simple element like hydrogen.
Mathematical Model
The primary basis for our understanding of the process of spontaneous photon emission comes from the law of conservation of energy, [math]\displaystyle{ {E}_{final} = {E}_{initial} }[/math].
When an atom decreases its energy level, as they do during spontaneous photon emission, this energy cannot be lost, in accordance with the law of conservation of energy. Instead, it is simply converted into another form, in this case, the kinetic energy of a photon. Because this process only involves two different particles, the atom and the photon, the law of conservation of energy also allows us to know that the change in the energy of the atom, is equal and opposite the change in the energy of the photon, [math]\displaystyle{ {Δ}{E}_{atom} = {-}{Δ}{E}_{photon} }[/math].
A Computational Model
 <https://www.https://phet.colorado.edu/en/simulations/lasers>
<https://www.https://phet.colorado.edu/en/simulations/lasers>
The above simulation from Physics Education Technology demonstrates the use of spontaneous photon emission in the starting of laser technology.
The number and distance between energy levels can be manipulated to observe their effect on the protons emitted and vice versa. The photon emitter power can be manipulated to observe the effect on the electron's energy (a display of stimulated photon emission)
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Simple
The energy of an atom decreases from -2 to -8 eV. A photon is emitted during this process, what is the energy of this photon?
[math]\displaystyle{ {E}_{photon} = {-}{Δ}{E}_{atom} = {-}{(}{E}_{f} - {E}_{i}{)} = {-}{(}{-8} - {-2}{)} = {6}{eV} }[/math]
Middling
A hydrogen atom is in the state N=3, where N=1 is the ground state. What will be the energy of the photon emitted when this atom drops from the 3rd to 1st energy level?
[math]\displaystyle{ {E}_{3} = {-}{13.6}/{3^2} = {-}{1.5111}{eV} }[/math]
[math]\displaystyle{ {E}_{1} = {-}{13.6}/{1} = {-}{13.6}{eV} }[/math]
[math]\displaystyle{ {E}_{photon} = {-}{Δ}{E}_{atom} = {-}{(}{E}_{1} - {E}_{3}{)} = {-}{(}{13.6} - {1.5111}{)} = {12.0889}{eV} }[/math]
Difficult
If electrons with energies of 10.27 volts collide with hydrogen atoms in their ground state, what will be the energy of the photons emitted by these atoms?
[math]\displaystyle{ {E}_{1} = {-}{13.6}/{1} = {-}{13.6}{eV} }[/math]
[math]\displaystyle{ {E}_{2} = {-}{13.6}/{2^2} = {-}{3.4}{eV} }[/math]
[math]\displaystyle{ {E}_{photon} = {-}{Δ}{E}_{atom} = {-}{(}{E}_{1} - {E}_{2}{)} = {-}{(}{13.6} - {3.4}{)} = {10.2}{eV} }[/math]
Because 10.2 < 10.27, the electrons will be able to excite the atoms to this energy level, and photons of energy 10.2 eV will be released when these atoms return to their ground state.
What will be the energy of the electrons after the collision?
Because [math]\displaystyle{ {Δ}{E}_{total} = {0} }[/math]
[math]\displaystyle{ {E}_{electron final} = {E}_{electron initial} - {Δ}{E}_{atom} = {10.27} - {10.2} = {.07}{eV} }[/math]
Connectedness
The primary use of spontaneous photon emission in industry is in the creation of products that center around the emission of light, such as fluorescent lights, light emitting diodes, and plasma TV screens. This process allows for the production of photons through the energizing of atoms, and can be extremely helpful for creating controlled light sources.
History
The concept of spontaneous emission was first theorized and observed by Albert Einstein, who accurately predicted that an atom may return to a lower energy level by emitting a photon. Einstein also proposed the concept that photons would tend to travel together in the same state. He theorized that a photon with a certain wavelength could pass through a field of atoms, leading to the emission of a photon with that same wavelength by the atoms. He predicted that this would lead to a ripple effect throughout this collection of atoms, that would lead to the production of photons of this same wavelength by all the surrounding atoms. This concept was first addressed in a paper written by Einstein in 1917, but was not put to use fully until the 1940s, when Charles Townes and Arthur Schawlow developed the first functioning laser.
See also
Quantized Energy Levels: http://www.physicsbook.gatech.edu/Quantized_energy_levels
External links
[1] [a href="https://www.rp-photonics.com/spontaneous_emission.html"]
References
"Emission Spectrum." Wikipedia. Wikimedia Foundation, 29 Nov. 2015. Web. 05 Dec. 2015.
"This Month in Physics History." : Einstein Predicts Stimulated Emission. American Physical Society, Aug.-Sept. 2005. Web. 05 Dec. 2015.
"Spontaneous Emission." Encyclopedia of Laser Physics and Technology. RP Photonics Encyclopedia, n.d. Web. 05 Dec. 2015. <https://www.rp-photonics.com/spontaneous_emission.html>.
"Spontaneous Emission." Spontaneous Emission. The University of Texas as Austin, n.d. Web. 05 Dec. 2015. <http://farside.ph.utexas.edu/teaching/qmech/Quantum/node119.html>.
"Spontaneous Emission." Wikipedia. Wikimedia Foundation, 4 Sept. 2015. Web. 05 Dec. 2015.