Conservation of Energy

Editor: Ethan Nguyen-Tu, Spring 2023

What is the Law of Conservation of Energy?
The Law of Conservation of Energy states that energy cannot be created or destroyed, but it can change from one form of energy to another.

Main Ideas

• The law of conservation of energy states that the total amount of energy of a system before and after an interaction between objects in conserved.
• This only applies to isolated systems (no outside forces acting on the system).
  • Not Isolated: An object sliding across a rough floor (system = the object). There is work being done by the floor on the object because of the frictional force. Energy lost to heat due to friction is an example of mechanical energy being converted into thermal energy.
  • Isolated: An object sliding across a rough floor (system = the object AND the floor). There is no work done on the system because all the forces are contained in the system.

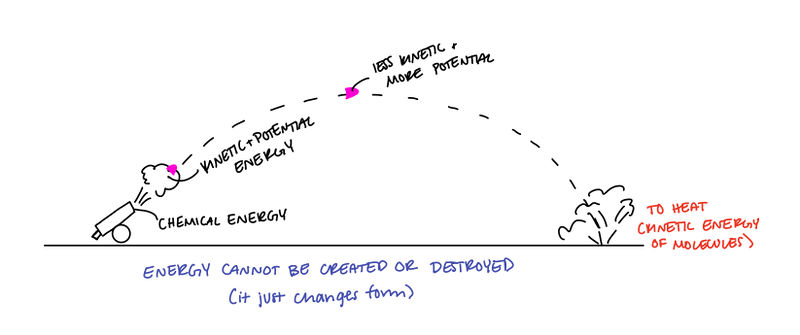
What does it mean?

Since The Law of Conservation of Energy states energy cannot be created or destroyed, this means that the total energy in the universe is constant and does not change in value.
Therefore, in equation format:    [math]\displaystyle{ \Delta E_{total, universe} = 0 }[/math]     [e.1]

Mathematical Model

[e.1]    [math]\displaystyle{ \Delta E_{total, universe} = 0 }[/math]
[e.3]    [math]\displaystyle{ \Delta E_{total, universe} = \Delta E_{system} + \Delta E_{surroundings} }[/math]

[e.1] & [e.3]:

[e.4]    [math]\displaystyle{ \Delta E_{system} + \Delta E_{surroundings} = 0 }[/math]

Isolated System

• ΔE = W + Q (if no heat transfer indicated, Q = 0; if no external forces acting on system, W = 0)
• ΔE = K + U (The total energy is the sum of the kinetic and potential energies. From this, you can infer that for an isolated system, any change in kinetic energy will correspond in an equal but opposite change in the potential energy and vice versa.)

These formulas can be interchanged. For example, if you know work and heat transfer are zero, energy equals zero, so K + U will equal zero

Basic Explanation of Conservation of Energy
Skater Visualization of Transfers of Energy

Computational Model

These gifs demonstrate the energy principal from a Conservation of Energy standpoint. As the ball on a spring approaches the equilibrium point, the kinetic energy increases and the spring potential decreases. These values will oscillate, but the total energy will stay constant! This demonstration was written in GlowScript and iteratively updates the ball's momentum while taking into account the spring force.

Useful Energy Formulas

Kinetic Energy

• Kinetic Energy: [math]\displaystyle{ {E_{kinetic} = K = \frac{1}{2}m\overrightarrow{v}^2} }[/math]

Potential Energy

• Gravitational Potential: [math]\displaystyle{ {U_{gravity} = U_g = \frac{Gm_1m_2}{ \big{|} \overrightarrow{r} \big{|}}(-\hat{r})} }[/math]
  • Approximation when near the Earth's Surface: [math]\displaystyle{ {\Delta U_g=mg\Delta h} }[/math]
• Spring (Elastic) Potential: [math]\displaystyle{ {U_{spring} = U_s = \frac{1}{2}k_ss^2} }[/math]

Thermal Energy

• Thermal Energy: [math]\displaystyle{ {\Delta E_{thermal} = mC \Delta T } }[/math]

Examples

Easy

A ball is at rest on a table with 50 J of potential energy. It then rolls off the table, and at one point in time as it falls, the ball has 30 J of kinetic energy.
What is the potential energy of the ball at that instant?

See Reference 3

E_initial = E_final
K_initial + U_initial = K_final + U_final
0 J + 50 J = 30 J + U_final
U_final = 20 J

Medium

A ball is at rest 50 m above the ground. You then drop the ball.
What is its speed before hitting the ground?

Hard

The driver of an SUV (m = 1700 kg) isn’t paying attention and rear ends a car (m = 950 kg) on level ground at a red light. On impact, both drivers lock their brakes. The SUV and car stick together and travel a distance of 8.2 m before they come to a stop. The coefficient of friction between the tires and the road is 0.72.
How fast was the SUV traveling just before the collision?

Connectedness

How does it relate to things we want to study?

In Physics, we separate what we are looking at into a system and its surroundings. This is a zero-sum separation where what we are interested in is included in the system and everything else in the universe is lumped into the system's surroundings.

In equation format:    Universe = System + Surroundings     [e.2]

This division of the universe into a system and its surroundings can also be applied to the total energy in the universe.

Therefore:    [math]\displaystyle{ \Delta E_{total, universe} = \Delta E_{system} + \Delta E_{surroundings} }[/math]     [e.3]

When trying to apply the Law of Conservation of Energy to [e.3], we run into an important problem:

When considering a system, is that it is highly time inefficient, and essentially impossible, to consider and factor in everything in the universe that is not included in the system. Therefore, this means that we can only find completely accurate values by applying the Law of Conservation of Energy to isolated systems in which the system has no net external force and does not exchange matter and energy with its surroundings. Nevertheless, applying the Law of Conservation of Energy to closed systems, in which matter is not able to enter or leave but energy can, we can get close approximations by identifying the main actors in the surroundings that influence our system.

How does it related to The Energy Principle?

Since the Law of Conservation of Energy says energy cannot be created or destroyed, The Energy Principle tells us that the only way for a system to gain or lose energy is from its surroundings losing or gaining the same amount of energy. Therefore, The Energy Principle can be generalized in terms of conservation of energy.

Written in equation form, The Energy Principle in terms of the Law of Conservation of Energy is:    [math]\displaystyle{ {\Delta E_{system}+\Delta E_{surroundings}=0} }[/math]     [e.4]

History

Who: Many physicists contributed to the knowledge of energy, however it is most notably attributed to Julius Robert Mayer
What: Most formally discovered the law of conservation of energy
When: 1842
Where: Germany
Why: To explain what happens to energy in an isolated system
See Reference 6

See also

• The Energy Principle
• Kinetic Energy
• Potential Energy
• Work

Additional Reading

1. Goldstein, Martin, and Inge F., (1993). The Refrigerator and the Universe. Harvard Univ. Press. A gentle introduction.
2. Kroemer, Herbert; Kittel, Charles (1980). Thermal Physics (2nd ed.). W. H. Freeman Company. ISBN 0-7167-1088-9.
3. Nolan, Peter J. (1996). Fundamentals of College Physics, 2nd ed. William C. Brown Publishers.

External Links

1. Khan Academy
2. Practice Questions
3. More Practice
4. Basic Examples
5. The First Law of Thermodynamics

References

1. "Conservation of Energy." Hmolpedia. Web. 1 Dec. 2015. <http://www.eoht.info/page/Conservation+of+energy>.
2. "University of Wisconsin Green Bay." Speed & Stopping Distance of a Roller-Coaster. Web. 1 Dec. 2015. <http://www.uwgb.edu/fenclh/problems/energy/2/>.
3. "Motion." G9 to Engineering. Web. 1 Dec. 2015. <http://www.g9toengineering.com/resources/translational.htm>.
4. "Energy of Falling Object." HyperPhysics. Web. 1 Dec. 2015. <http://hyperphysics.phy-astr.gsu.edu/hbase/flobj.html>.
5. "Conservation of Energy & Momentum Problem: Collision of Two Cars at a Stoplight." University of Wisconsin- Green Bay Physics. Web. 2 Dec. 2015. <http://www.uwgb.edu/fenclh/problems/energy/6/>.
6. "Law of Conservation of Mass Energy." Law of Conservation of Mass Energy. Web. 3 Dec. 2015. <http://www.chemteam.info/Thermochem/Law-Cons-Mass-Energy.html>.
7. "Law of Conservation of Energy" New York University. Web. 18 Apr. 2018. <http://www.nyu.edu/classes/tuckerman/adv.chem/lectures/lecture_2/node4.html>
8. "Law of Conversation of Energy" ME Mechanical. Web. 18 Apr. 2018. <https://me-mechanicalengineering.com/law-of-conservation-of-energy/>