Terminal Velocity and Friction Due to Air: Difference between revisions
No edit summary |
|||
| Line 60: | Line 60: | ||
===Examples=== | ===Examples=== | ||
'''Skydiver''': Think of a free-falling skydiver. When he/she is falling with their arms and legs stretched out like a star, they will accelerate until he or she reaches their terminal velocity. Now, what would happen if the free-faller pulled in his/her arms and legs and leans forward so that their body is more parallel with their free-fall? From our definition of terminal velocity defined above, we know that this speed is inversely dependent on the surface area of the falling object. So, we can infer that the skydiver would speed up, because when he/she bring their arms and legs in, they decrease their surface area perpendicular to the fall and therefor increase their terminal velocity. | '''Skydiver''': Think of a free-falling skydiver. When he/she is falling with their arms and legs stretched out like a star, they will accelerate until he or she reaches their terminal velocity. Now, what would happen if the free-faller pulled in his/her arms and legs and leans forward so that their body is more parallel with their free-fall? From our definition of terminal velocity defined above, we know that this speed is inversely dependent on the surface area of the falling object. So, we can infer that the skydiver would speed up, because when he/she bring their arms and legs in, they decrease their surface area perpendicular to the fall and therefor increase their terminal velocity. | ||
[[File:Skydiver2.jpg|thumb|center|600x310px]] | |||
'''Heat of Spacecraft''': Think of a spacecraft re-entering the Earth's atmosphere. How would the engineers designing that spacecraft need to determine the temperature that the space craft material needs to withstand. Well, these engineers could use the energy principle and the specific heat of the building material to do so. By calculating the terminal velocity, the initial potential and kinetic energy of the space craft when it enters the Earth's gravitational pull, and then graphing all the energy as at the space ship plummets to Earth's surface, these engineers can determine the heat this building material must be able to withstand. | '''Heat of Spacecraft''': Think of a spacecraft re-entering the Earth's atmosphere. How would the engineers designing that spacecraft need to determine the temperature that the space craft material needs to withstand. Well, these engineers could use the energy principle and the specific heat of the building material to do so. By calculating the terminal velocity, the initial potential and kinetic energy of the space craft when it enters the Earth's gravitational pull, and then graphing all the energy as at the space ship plummets to Earth's surface, these engineers can determine the heat this building material must be able to withstand. | ||
Revision as of 10:24, 30 November 2015
claimed by cshimkus3
Acceleration of Falling Objects
When you drop an object from a certain height off the ground, you can observe that the speed of the object does not remain constant throughout that object's free fall. The object's speed changes as it falls and we know from the momentum principle that this is due to a net force acting on the object( Fnet = dp/dt ). If you drop an object from a tall enough starting height, you can also observe that the acceleration of the object is not constant either, so one can conclude that the net force on the object is not constant. An object falling towards the Earth's surface will not accelerate indefinitely, but will reach what is called ' ' terminal velocity ' '. Odds are you are familiar with the force of gravity, the force that holds you to Earth's surface and causes an object to accelerate initially downward. Gravity is defined as F=mg, where g is the acceleration constant of 9.8 m/s^2 (on Earth), and is a constant force. Another force, friction, is also acting on a falling object, however. This friction is due to the contact between molecules of the falling object and air molecules and is non-constant through the objects free-fall. In the following sections we will look into greater detail the effects of friction due to air.
Falling Objects in a Vacuum
As stated above, the force due to gravity on an object is constant. This can be proven by an object that is in free fall and is also in a vacuum. When an object is falling within a vacuum, it can be observed to have constant acceleration of 9.8 m/s^2 regardless of its mass or size. In the following video, a feather and a ball bearing are dropped inside a vacuum. See how both objects fall at the same rate. (Click on the picture)
Friction Due to Air
The friction due to air is a non-constant force on a falling object, and is related to multiple factors, such as cross-sectional area, the objects velocity, and the density of air. The force of air on a falling object is defined by the following equation in the opposite direction of the objects motion:
C is the numerical drag coeffecient which is dependent on the shape of the object.
So, when the force of air comes into play, we see the the feather and ball bearing will not fall at the same rate because they have different cross sectional areas. The following video shows a feather and ball bearing being dropped in both scenarios.
As stated above, the force of air on a falling object is also dependent on the speed of a falling object. In that respect, we come to discuss terminal velocity. The force of air increases quadraticly with the speed of a falling object, so while the force of gravity remains constant, the force of air resistance will increase until the two forces perfectly cancel each other out and the net force is zero. At this point, the acceleration of an object is zero and the object has reached terminal velocity. You may ask "Why will the force of air not exceed the force of gravity?". This is because the force of air only continues to increase as the speed of the falling object increases and as the magnitude of the net force decreases, the speed of the object will approach being constant. Therefor, the magnitude of the force of air will also approach being constant. An object's terminal velocity can be defined by the following equation:
Where does that energy go?
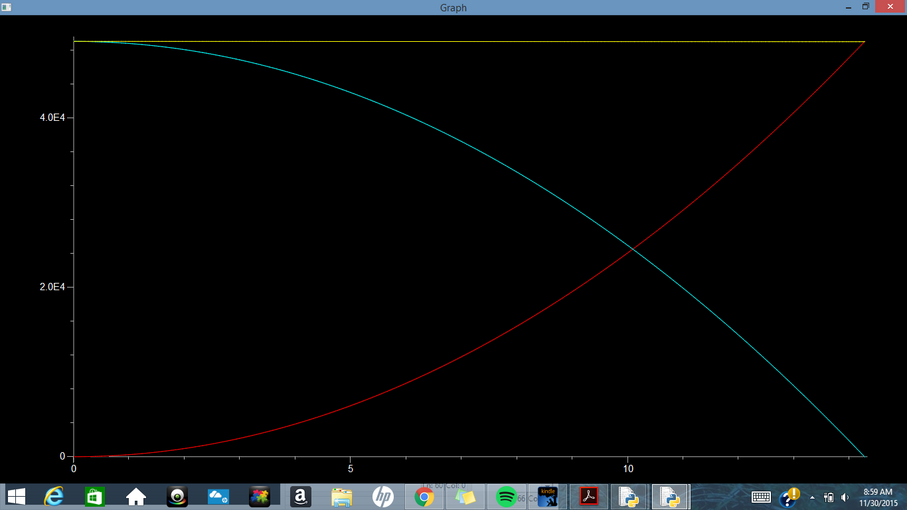
When we think of the energy of a falling object from the stance of a point-particle system, it will seem that some of the energy will disappear. When a falling object reaches terminal velocity, its kinetic energy remains constant while its potential energy due to gravity decreases. So, where does this energy go? We can now think of the falling object as an extended system and see that this energy get converted to internal energy as heat. The friction between the air and the falling object creates heat that takes the form of the lost energy. In a vacuum, this would not happen. The gravitational and kinetic energy of an object in a vacuum would vary inversely with one another.
A Graphical Interpretation
The following graphs will help you better understand the motion and energy relationships of a falling object.
A) 5 kg Ball Falling in Vacuum: Velocity vs Height
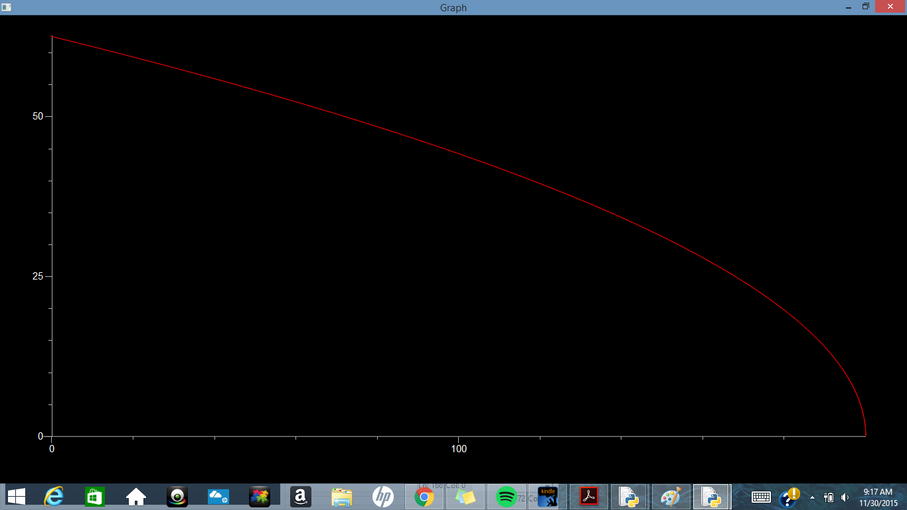
B) 5 kg Ball Falling in Air
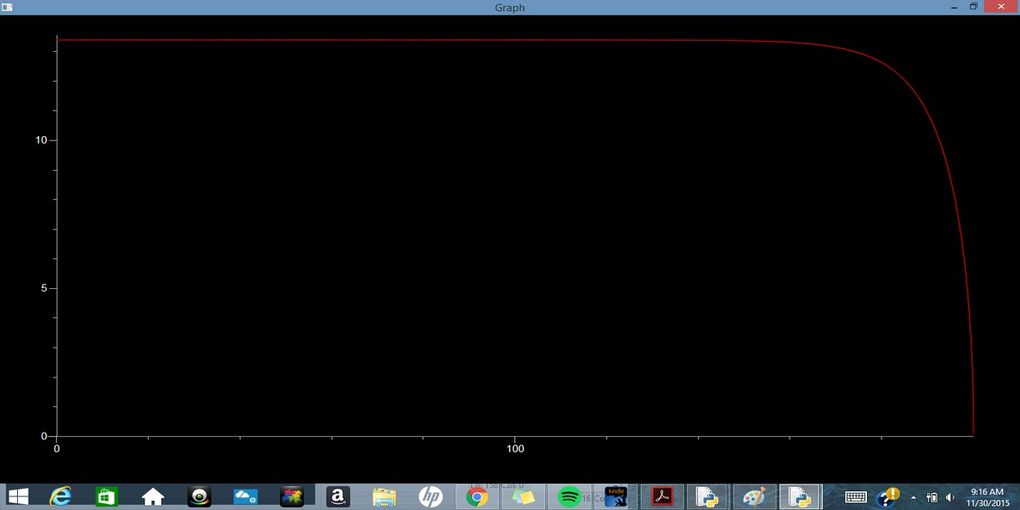
C) .5 kg Feather Falling in Vacuum

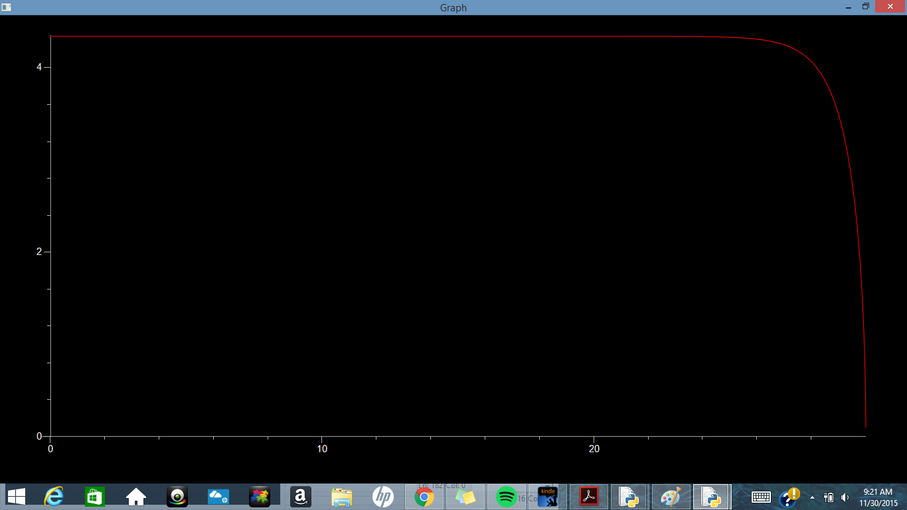
D) .5 kg Feather Falling in Air
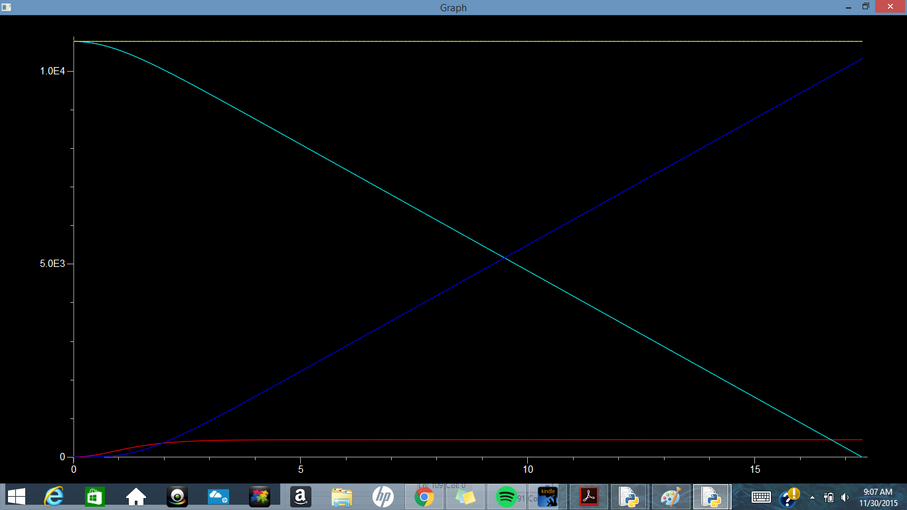
E) Energy of Ball Falling in Vacuum: Energy vs Time (yellow=total, red=kinetic, blue=thermal, cyan=potential)
F) Energy of Ball Falling in Air
Examples
Skydiver: Think of a free-falling skydiver. When he/she is falling with their arms and legs stretched out like a star, they will accelerate until he or she reaches their terminal velocity. Now, what would happen if the free-faller pulled in his/her arms and legs and leans forward so that their body is more parallel with their free-fall? From our definition of terminal velocity defined above, we know that this speed is inversely dependent on the surface area of the falling object. So, we can infer that the skydiver would speed up, because when he/she bring their arms and legs in, they decrease their surface area perpendicular to the fall and therefor increase their terminal velocity.

Heat of Spacecraft: Think of a spacecraft re-entering the Earth's atmosphere. How would the engineers designing that spacecraft need to determine the temperature that the space craft material needs to withstand. Well, these engineers could use the energy principle and the specific heat of the building material to do so. By calculating the terminal velocity, the initial potential and kinetic energy of the space craft when it enters the Earth's gravitational pull, and then graphing all the energy as at the space ship plummets to Earth's surface, these engineers can determine the heat this building material must be able to withstand.
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
Thermodynamics was brought up as a science in the 18th and 19th centuries. However, it was first brought up by Galilei, who introduced the concept of temperature and invented the first thermometer. G. Black first introduced the word 'thermodynamics'. Later, G. Wilke introduced another unit of measurement known as the calorie that measures heat. The idea of thermodynamics was brought up by Nicolas Leonard Sadi Carnot. He is often known as "the father of thermodynamics". It all began with the development of the steam engine during the Industrial Revolution. He devised an ideal cycle of operation. During his observations and experimentations, he had the incorrect notion that heat is conserved, however he was able to lay down theorems that led to the development of thermodynamics. In the 20th century, the science of thermodynamics became a conventional term and a basic division of physics. Thermodynamics dealt with the study of general properties of physical systems under equilibrium and the conditions necessary to obtain equilibrium.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
Internet resources on this topic
References
https://www.grc.nasa.gov/www/k-12/airplane/thermo0.html http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/thereq.html https://www.grc.nasa.gov/www/k-12/airplane/thermo2.html http://www.phys.nthu.edu.tw/~thschang/notes/GP21.pdf http://www.eoearth.org/view/article/153532/



