Second Law of Thermodynamics and Entropy: Difference between revisions
Pearlruparel (talk | contribs) |
Pearlruparel (talk | contribs) |
||
| Line 11: | Line 11: | ||
What are the mathematical equations that allow us to model this topic. For example <math>\deltaV = -\left(E_x * \deltax + E_y * \deltay + E_z * \deltaz \right) </math> where '''E''' is the electric field with components in the x, y, and z directions. Delta x, y, and z are the components of final location minus to the components of the initial location. | What are the mathematical equations that allow us to model this topic. For example <math>\deltaV = -\left(E_x * \deltax + E_y * \deltay + E_z * \deltaz \right) </math> where '''E''' is the electric field with components in the x, y, and z directions. Delta x, y, and z are the components of final location minus to the components of the initial location. | ||
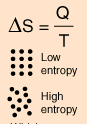
Entropy is a state variable whose change is defined for a reversible process at T where Q is the heat absorbed. It can be calculated for a reaction using the equation \deltaS = Q / T where Q is the heat absorbed for temperature T. | |||
[[File:Screen_Shot_2015-11-30_at_2.50.57_PM.png ]] | |||
===A Computational Model=== | ===A Computational Model=== | ||
Revision as of 14:57, 30 November 2015
by Pearl Ruparel
Second Law of Thermodynamics
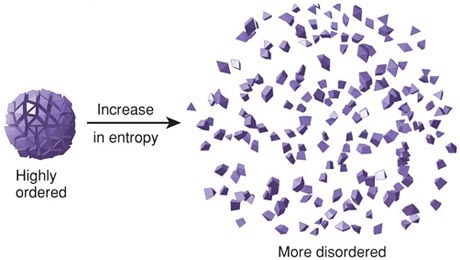
Thermodynamics is a huge area of physics that deals with study of effects of work, heat, and energy on a system. It is concerned with large scale observations. There is zeroth law, first law, and second law of thermodynamics. The zeroth law involves simple definition of thermodynamic equilibrium while the first law deals mainly with kinetic and potential energy and transfer of heat and internal energy while introducing enthalpy which leads to second law of thermodynamics. The second law of thermodynamics stipulates that the total entropy of a system plus its environment can not decrease; it can remain constant for a reversible process but must always increase for an irreversible process. Entropy is described as measure of disorder in a closed system/ thermal energy not available to do work.
A Mathematical Model
What are the mathematical equations that allow us to model this topic. For example [math]\displaystyle{ \deltaV = -\left(E_x * \deltax + E_y * \deltay + E_z * \deltaz \right) }[/math] where E is the electric field with components in the x, y, and z directions. Delta x, y, and z are the components of final location minus to the components of the initial location.
Entropy is a state variable whose change is defined for a reversible process at T where Q is the heat absorbed. It can be calculated for a reaction using the equation \deltaS = Q / T where Q is the heat absorbed for temperature T.
A Computational Model
How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Simple
Middling
Difficult
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
Internet resources on this topic
References
This section contains the the references you used while writing this page