Series Circuits: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| Line 5: | Line 5: | ||
:The electrical connection is not branched in any way. One can visualize this circuit as simply a closed loop. | :The electrical connection is not branched in any way. One can visualize this circuit as simply a closed loop. | ||
:Often times, the simple series circuit may include but are not limited to: a number of resistors, switches, and of course, batteries. | :Often times, the simple series circuit may include but are not limited to: a number of resistors, switches, and of course, batteries. | ||
:Keep in mind, if there is an open switch or break in the circuit no current flows. | |||
===A Mathematical Model=== | ===A Mathematical Model=== | ||
| Line 24: | Line 25: | ||
:The best way to visualize a series circuit is to draw a schematic, which is a simplified representation of the circuit in real life. | :The best way to visualize a series circuit is to draw a schematic, which is a simplified representation of the circuit in real life. | ||
:Resistors are usually represented by | :Resistors are usually represented in a schematic with [[File:Resistor Symbol.png|100px]] | ||
:Batteries are represented in a schematic by [[File:Schematic-symbols-battery.png|75px]] | |||
:Switches can be open or closed. An open switch is represented by [[File:Schematic-symbols-switch.png|75px]] | |||
==Examples== | ==Examples== | ||
Revision as of 15:56, 30 November 2015
claimed by Mchan46
Main Idea
- A Series Circuit is a simple type of electrical circuit in which components are placed in succession of one another.
- The electrical connection is not branched in any way. One can visualize this circuit as simply a closed loop.
- Often times, the simple series circuit may include but are not limited to: a number of resistors, switches, and of course, batteries.
- Keep in mind, if there is an open switch or break in the circuit no current flows.
A Mathematical Model
- Kirchhoff's Current and Voltage Laws apply in a series circuit.
- Through Kirchhoff's Current Law, we know that the sum of all current going in must equal the sum of all current going out.
- [math]\displaystyle{ \sum{I}_{in} - \sum{I}_{out} = 0 }[/math]
- Since there are no nodes for the current to split up, the current throughout a series circuit will always be the same through each component.
- Through Kirchhoff's Voltage Law, the sum of all voltage in a closed system must be zero.
- [math]\displaystyle{ \sum{V}_{Battery} - \sum{V}_{Components} = 0 }[/math]
- Through Kirchhoff's Current Law, we know that the sum of all current going in must equal the sum of all current going out.
- Ohm's Law is extremely useful in finding the voltages, resistances, and current throughout the series circuit.
- Ohm's Law gives us the following formula:
- [math]\displaystyle{ V=IR }[/math]; it can be rearranged to yield [math]\displaystyle{ I=\frac{V}{R} }[/math] and [math]\displaystyle{ R = \frac{V}{I} }[/math]
- Ohm's Law gives us the following formula:
A Computational Model
- The best way to visualize a series circuit is to draw a schematic, which is a simplified representation of the circuit in real life.
- Resistors are usually represented in a schematic with

- Batteries are represented in a schematic by

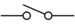
- Switches can be open or closed. An open switch is represented by
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Simple
Middling
Difficult
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
Internet resources on this topic
References
This section contains the the references you used while writing this page