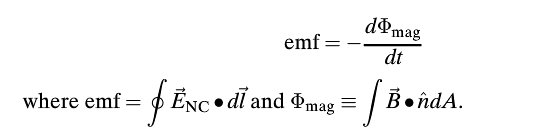Faraday's Law

Claimed by Cristina Guruceaga (cguruceaga3)

Faraday's Law of Induction

This topics focuses on the electric field associated with a time-varying magnetic field. Faraday's Law makes the connection between electric and magnetic field.

Faraday's Law summarizes the ways voltage can be generated.  

Faraday's law is a fundamental relationship which comes from Maxwell's equations. It serves as a succinct summary of the ways a voltage (or emf) may be generated by a changing magnetic environment. The induced emf in a coil is equal to the negative of the rate of change of magnetic flux times the number of turns in the coil. It involves the interaction of charge with magnetic field.

Faraday's Law Experiment

Faraday showed that no current is registered in the galvanometer when bar magnet is stationary with respect to the loop. However, a current is induced in the loop when a relative motion exists between the bar magnet and the loop. In particular, the galvanometer deflects in one direction as the magnet approaches the loop, and the opposite direction as it moves away.

Faraday’s experiment demonstrates that an electric current is induced in the loop by changing the magnetic field. The coil behaves as if it were connected to an emf source. Experimentally it is found that the induced emf depends on the rate of change of magnetic flux through the coil.

Mathematical Equation

Faraday's Law Equation

In other words: The emf along a round-trip is equal to the rate of change of the magnetic flux on the area encircled by the path.

Direction: With the thumb of your right hand pointing in the direction of the -dB/dt, your fingers curl around in the direction of Enc.

The meaning of the minus sign: If the thumb of your right hand points in the direction of -dB/dt (that is, the opposite of the direction in which the magnetic field is increasing), your fingers curl around in the direction along which the path integral of electric field is positive. Similarly it can be explained using Lenz's Law. The direction of the induced current is determined by Lenz’s law which states that the induced current produces magnetic fields which tend to oppose the changes in magnetic flux that induces such currents.

Formal Version of Faraday's Law

Examples

Reversible process: Ideally forcing a flow through a constricted pipe, where there are no boundary layers. As the flow moves through the constriction, the pressure, volume and temperature change, but they return to their normal values once they hit the downstream. This return to the variables' original values allows there to be no change in entropy. It is often known as an isentropic process.

Irreversible process: When a hot object and cold object are put in contact with each other, eventually the heat from the hot object will transfer to the cold object and the two will reach the same temperature and stay constant at that temperature, reaching equilibrium. However, once those objects are separated, they will remain at that equilibrium temperature until something else acts upon it. The objects do not go back to their original temperatures so there is a change in entropy.

Problem Solving Tips

In this chapter we have seen that a changing magnetic flux induces an emf:

according to Faraday’s law of induction. For a conductor which forms a closed loop, the emf sets up an induced current I =|ε |/R , where R is the resistance of the loop. To compute the induced current and its direction, we follow the procedure below:

1. For the closed loop of area on a plane, define an area vector A and let it point in the direction of your thumb, for the convenience of applying the right-hand rule later. Compute the magnetic flux through the loop using

Determine the sign of the magnetic flux Φ

2. Evaluate the rate of change of magnetic flux dΦ/dt . Keep in mind that the change could be caused by

Determine the sign of

3. The sign of the induced emf is the opposite of that of / B dΦ d . The direction of the induced current can be found by using Lenz’s law or right hand rule (discussed previously).

Connectedness

1. How is this topic connected to something that you are interested in?
2. How is it connected to your major?
3. Is there an interesting industrial application?

History

Michael Faraday was an English physicist working in the early 1800's. He worked with another scientist named Sir Humphrey Davy. Faraday's big discovery happened in 1831 when he found that when you change a magnetic field, you can create an electric current. He did a lot of other work with electricity such as making generators and experimenting with electrochemistry and electrolysis.

Faraday's experiments started with magnetic fields that stayed the same. That setup did not induce current. It was only when he started to change the magnetic fields that the current and voltage were induced (created). He discovered that the changes in the magnetic field and the size of the field were related to the amount of current created. Scientists also use the term magnetic flux. Magnetic flux is a value that is the strength of the magnetic field multiplied by the surface area of the device.

See also

To fully understand this topic, you need to have an understanding on Maxwell's equations and Lenz's Law.

Further reading

Books, Articles or other print media on this topic

External links

Faraday's Law Simulation: https://phet.colorado.edu/en/simulation/faradays-law

References

Encyclopedia.com: http://www.encyclopedia.com/topic/Faradays_law.aspx Wikipedia (Electromagnetic Induction): http://en.wikipedia.org/wiki/Electromagnetic_induction Encyclopædia Britannica (Faraday's Law of Induction): http://www.britannica.com/EBchecked/topic/201744/Faradays-law-of-induction