Ampere-Maxwell Law

Claimed by Maria Rivero

Ampere-Maxwell Law

James Maxwell discovered that a time-varying electric field could be accompanied by a magnetic field. He thought of this after Faraday discovered that a time-varying magnetic field was accompanied by an electric field.

The time rate that is used for this equation is given by the derivative of the electric flux with respect to time. Because The derivative of the flux gives current over epsilon nod, the derivative of the electric flux times epsilon nod will also have units of amperes.

Where B is the magnetic field dl is the change in path The sum of I is the sum of the charges inside the path.

Example

Pick a closed, rectangular path in the xz plane with a height h and a width w. Calculate the speed v of the slab.

At a time change in t, we can calculate the area as the height (h) times the speed over the change in time. ⩟ A = v (⩟ t) h Because the electric field is constant in this region we can also calculate the change in electric flux over time as Evh(⩟ t) /(⩟ t) which is the same as Evh Calculating the path integral for the magnetic field we get that ∮B . dl = Bh cos 0 = Bh An important thing to notice is that there is no current I, so, using the Ampere-Maxwell Law we can see that

Bh = μ. [I+ ε. (vEh)]

but since there is no current,

B = μ. ε. (vE)

From Faraday's law we get that the emf equals the rate of change of the magnetic flux: Eh = Bvh

Substituting E = Bv into our previous equation we get that

B = μ. ε. (v(vB))

Solving for v we get that:

From the picture we see that the speed of light relates the a time varying electric and magnetic field.

A Mathematical Model

In order to find the potential difference between two locations, we use this formula [math]\displaystyle{ dV = -\left(E_x*dx + E_y*dy + E_z*dz\right) }[/math], where E is the electric field with components in the x, y, and z directions. Delta x, y, and z are the components of final location minus to the components of the initial location.

A Computational Model

How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript

Simple Example

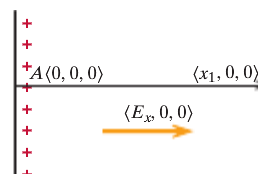
In this example, the electric field is equal to [math]\displaystyle{ E = \left(E_x, 0, 0\right) }[/math]. The initial location is A and the final location is C. In order to find the potential difference between A and C, we use [math]\displaystyle{ dV = V_C - V_A }[/math].

Since there are no y and z components of the electric field, the potential difference is [math]\displaystyle{ dV = -\left(E_x*\left(x_1 - 0\right) + 0*\left(-y_1 - 0\right) + 0*0\right) = -E_x*x_1 }[/math]

Let's say there is a location B at [math]\displaystyle{ \left(x_1, 0, 0\right) }[/math]. Now in order to find the potential difference between A and C, we need to find the potential difference between A and B and then between B and C.

The potential difference between A and B is [math]\displaystyle{ dV = V_B - V_A = -\left(E_x*\left(x_1 - 0\right) + 0*0 + 0*0\right) = -E_x*x_1 }[/math].

The potential difference between B and C is [math]\displaystyle{ dV = V_C - V_B = -\left(E_x*0 + 0*\left(-y_1 - 0\right) + 0*0\right) = 0 }[/math].

Therefore, the potential difference A and C is [math]\displaystyle{ V_C - V_A = \left(V_C - V_B\right) + \left(V_B - V_A\right) = E_x*x_1 }[/math], which is the same answer that we got when we did not use location B.

Connectedness

1. How is this topic connected to something that you are interested in?
2. How is it connected to your major?
3. Is there an interesting industrial application?

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

External links

Internet resources on this topic

References

This section contains the the references you used while writing this page