Power in a circuit

Short Description of Topic

The Main Idea

Measuring the power in a circuit can provide useful insight into the ability of a circuit to accomplish a given task. In order to understand how to calculate and interpret power in a simple circuit, one must know the mechanical definition and significance of Power. For this section, we will be using the unit of Watt for power.

It is important to note that the power in parts of a circuit can be represented in several different ways. Most commonly, power in a circuit is expressed in terms of Voltage (E, Emf, Volts), Current (I, Amps), and Resistance (R, Ohms). It is typical to focus a discussion of power in a circuit around the power that is dissipated by a resistor. The power dissipated by a resistor directly coincides with the amount of energy that the resistor converts into non-electrical energy such as thermal or light energy.

A Mathematical Model

The power dissipated in a resistor is [math]\displaystyle{ P=IV }[/math] or [math]\displaystyle{ P=I^2R }[/math] or [math]\displaystyle{ P=V^2/R }[/math]

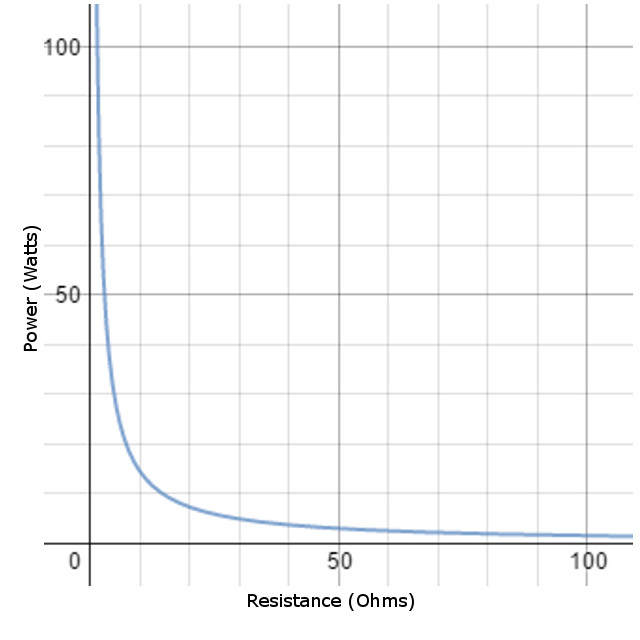
A Graphical Model

Here is a model of how the power dissipated changes as the resistance in a circuit is modified. This graph is based on a constant voltage of 12 volts.

From the graph, it becomes clear that as resistance increases, the power dissipated by the resistor decreases. This also graph models how using a potentiometer or variable resistor would effect the power dissipation in a 12 volt circuit.

Examples

3 varying examples.

Simple

A circuit with a steady voltage of 12 volts contains a 5 ohm resistor. How much power is dissipated by this resistor?

<math> P=V^2/R=12^2/5=28.8 watts

Connectedness

This topic is extremely important in examining infrastructure related to energy distribution. For example, in power grids, power lines are resistors, and therefore dissipate a certain amount of power. Since resistance is also related to the length of a wire, we can deduce that more power will be dissipated across longer power lines.

Additionally, it is extremely important to understand the concept of power dissipated by a resistor in the field of Electrical Engineering. For example, knowing how to calculate the power dissipated allows for the calculation of how large a resistor needs to be in order handle the energy dissipated over time through heat.

History

The discovery of how to calculate the power in a circuit is directly related to the discovery of Ohm's Law which relates voltage to resistance and current. Ohm's law was discovered by Georg_Ohm. The further development of the units for these three properties results in the derivation of the calculation for power dissipation in a circuit.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

External links

Internet resources on this topic

References

This section contains the the references you used while writing this page

http://mechatronics.mech.northwestern.edu/design_ref/sensors/potentiometers.html http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elepow.html https://openstaxcollege.org/files/textbook_version/low_res_pdf/9/CollegePhysics-LR.pdf http://micro.magnet.fsu.edu/electromag/java/ohmslaw/