Net Force

by Julia Logan

Definition

A Mathematical Model

In order to calculate net force, all EXTERNAL forces acting on a system are added together. The formal mathematical definition is [math]\displaystyle{ dV = -\left(E_x*dx + E_y*dy + E_z*dz\right) }[/math], where E is the electric field with components in the x, y, and z directions. Delta x, y, and z are the components of final location minus to the components of the initial location.

A Computational Model

Net force is an essential component of the Momentum Principle! We can use the Momentum Principle in vpython to update the position of a moving object. But first, we have to find net force.

  #1 Fspring = -k*s
  #2 Fgravmag = mball * g
  #3 Fgrav = Fgravmag * vector(0,-1,0)
  #4 Fnet = Fspring+Fgrav
  #5 pball = pball + Fnet * deltat
  #6 vball = pball / mball
  #7 ball.pos=ball.pos+vball*deltat

Here, the spring force and the gravitational force are found using formulas (lines 1-3). Then, they are added together to get the net force on the object (in this case a ball, line 4). The net force is then used in the update form of the momentum principle (line 5). In line 6 the velocity is updated, and line 7 the position is updated. Without net force calculations, tracing an object's path would be impossible.

File:Netforce.jpg

Simple Example

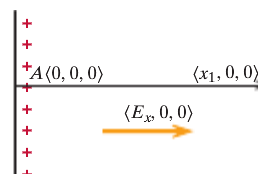
In this example, the electric field is equal to [math]\displaystyle{ E = \left(E_x, 0, 0\right) }[/math]. The initial location is A and the final location is C. In order to find the potential difference between A and C, we use [math]\displaystyle{ dV = V_C - V_A }[/math].

Since there are no y and z components of the electric field, the potential difference is [math]\displaystyle{ dV = -\left(E_x*\left(x_1 - 0\right) + 0*\left(-y_1 - 0\right) + 0*0\right) = -E_x*x_1 }[/math]

Let's say there is a location B at [math]\displaystyle{ \left(x_1, 0, 0\right) }[/math]. Now in order to find the potential difference between A and C, we need to find the potential difference between A and B and then between B and C.

The potential difference between A and B is [math]\displaystyle{ dV = V_B - V_A = -\left(E_x*\left(x_1 - 0\right) + 0*0 + 0*0\right) = -E_x*x_1 }[/math].

The potential difference between B and C is [math]\displaystyle{ dV = V_C - V_B = -\left(E_x*0 + 0*\left(-y_1 - 0\right) + 0*0\right) = 0 }[/math].

Therefore, the potential difference A and C is [math]\displaystyle{ V_C - V_A = \left(V_C - V_B\right) + \left(V_B - V_A\right) = E_x*x_1 }[/math], which is the same answer that we got when we did not use location B.

Connectedness

1. How is this topic connected to something that you are interested in?
2. How is it connected to your major?
3. Is there an interesting industrial application?

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

External links

Internet resources on this topic

References

This section contains the the references you used while writing this page