Amedeo Avogadro: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
Claimed by lchen353 | Claimed by lchen353 | ||
[[File:Amedeo_Avogadro2|thumb|right|Amedeo Avogadro]] | |||
=Bibliography= | =Bibliography= | ||
Revision as of 18:44, 30 November 2015
Claimed by lchen353
Bibliography
Amadeo Avagadro (Lorenze Romano Amedeo Carlo Avagadro, conte di Quaregna e Cerreto) was born on August 9, 1776 in Turin, Italy. Avogadro had initially started going to law school after his father's request and tradition, but soon after he was inspired to pursue a new path and committed his life to mathematics, physics, and chemistry. After finishing with a doctorate of ecclesiastical law in 1796, he privately began studying physics, and in 1806 he began teaching science and mathematics at the Academy of Sciences of Turin. Three years later he became a professor at the Royal College of Vercelli, but because of civil unrest the university was shut down and forced Avogadro to lose his chair position, only to regain his chair back in 1834. Avogadro died on July 9, 1856.
A Mathematical Model
In order to find the potential difference between two locations, we use this formula [math]\displaystyle{ dV = -\left(E_x*dx + E_y*dy + E_z*dz\right) }[/math], where E is the electric field with components in the x, y, and z directions. Delta x, y, and z are the components of final location minus to the components of the initial location.
A Computational Model
How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript
Simple Example
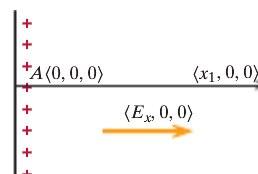
In this example, the electric field is equal to [math]\displaystyle{ E = \left(E_x, 0, 0\right) }[/math]. The initial location is A and the final location is C. In order to find the potential difference between A and C, we use [math]\displaystyle{ dV = V_C - V_A }[/math].
Since there are no y and z components of the electric field, the potential difference is [math]\displaystyle{ dV = -\left(E_x*\left(x_1 - 0\right) + 0*\left(-y_1 - 0\right) + 0*0\right) = -E_x*x_1 }[/math]
Let's say there is a location B at [math]\displaystyle{ \left(x_1, 0, 0\right) }[/math]. Now in order to find the potential difference between A and C, we need to find the potential difference between A and B and then between B and C.
The potential difference between A and B is [math]\displaystyle{ dV = V_B - V_A = -\left(E_x*\left(x_1 - 0\right) + 0*0 + 0*0\right) = -E_x*x_1 }[/math].
The potential difference between B and C is [math]\displaystyle{ dV = V_C - V_B = -\left(E_x*0 + 0*\left(-y_1 - 0\right) + 0*0\right) = 0 }[/math].
Therefore, the potential difference A and C is [math]\displaystyle{ V_C - V_A = \left(V_C - V_B\right) + \left(V_B - V_A\right) = E_x*x_1 }[/math], which is the same answer that we got when we did not use location B.
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
Internet resources on this topic
References
This section contains the the references you used while writing this page