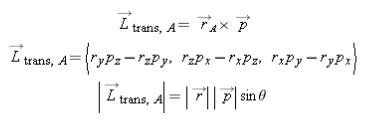The Angular Momentum Principle: Difference between revisions
| Line 43: | Line 43: | ||
== Examples == | == Examples == | ||
'''Simple''' | '''Simple''' | ||
[[File:simpleam.jpg]] | [[File:simpleam.jpg]] | ||
'''Middle''' | '''Middle''' | ||
[[File:middle1.png]] | [[File:middle1.png]] | ||
| Line 53: | Line 55: | ||
'''Difficult''' | '''Difficult''' | ||
[[File:difficult1.png]] | [[File:difficult1.png]] | ||
Revision as of 21:55, 30 November 2015
claimed by rhollman6
The Main Idea
The angular momentum of an object is the product of the moment of inertia and the angular velocity and is a vector quantity. Total angular momentum is equal to the translational angular momentum about a location A plus the rotational angular momentum around the object's center of mass. The angular momentum principle says that derivative of total angular momentum is equal to the torque applied to the object. Torque is equal to the force about a particular location A times the vector from location A to point of application of force (this is a vector product and torque is a vector quantity). Applying a torque to the system changes the angular momentum of the system. The change in angular momentum of a particle relative to location A is equal to the net angular impulse (net torque,A times the change in time). The angular momentum principle is similar to the momentum principle and the angular momentum principle can be used to calculate torque. Angular momentum is conserved so if system gains angular momentum, the surroundings lose that amount. If there is no torque (and therefore no force) applied to the system then the angular impulse is zero and initial angular momentum equals final angular momentum. The angular momentum principle allows you to learn information about initial angular momentum, final angular momentum, change in time and/or torque depending on what variables are known.
A Mathematical Model
Translational angular momentum is equal to the vector cross product of the location from the object pointing to the location A and the momentum of the object. It can also be found by multiplying the magnitude of the distance vector times the magnitude of the momentum vector times the sin of theta (the angle the two vectors make when they are put tail to tail).
Total angular momentum is equal to the sum of translational angular momentum about location A and rotational angular momentum about the object's center of mass. In multi-particle systems, the translational angular momentum is equal to the vector product of the distance of the center of mass to location A and total momentum of the whole system. Rotational angular momentum is equal to the vector product of the distance of particle 1 to center of mass and momentum of particle 1 plus the vector product of distance of particle 2 to center of mass and momentum of particle 2 plus all the particles in the system. If total angular momentum and translational angular momentum are known then rotational angular momentum can be found just by subtracting Ltrans from Ltot and if Ltot and Lrot are known, Ltrans can be found by subtracting Lrot from Ltot.
The total angular momentum of the system plus the total angular momentum of the surroundings is equal to zero and this is called the conservation of angular momentum. Angular momentum is conserved so if system gains angular momentum, the surroundings lose that amount.
The derivative of total angular momentum is equal to the torque around location A.
Torque is equal to the vector product of the distance from location A to the point of the application of the force and the force itself.
Torque can also be found by multiplying the magnitude of the direction vector from location A to the point of application of the force, the magnitude of the force applied and sin of theta. Theta is the angle the two vectors make when they are put tail to tail.
The angular momentum principle states that the change in total angular momentum in a system is equal to the torque applied to the system times the time the torque is applied. If there is no force acting on the system then there is no torque acting on the system so change in total angular momentum of the system is equal to zero.
Another way of writing the angular momentum principle is the final total angular momentum is equal to the initial total angular momentum plus the angular impulse. This is true because the change in total angular momentum is equal to final total angular momentum minus initial total angular momentum and you can add initial total angular momentum to the other side of the equation to get this equation. Once again, if there is no force acting on the system then there is no torque acting on the system and the angular impulse is equal to zero so final total angular momentum equals initial total angular momentum.
A Computational Model
This vPython code shows how to solve for final total angular momentum of an object (in this case a comet orbiting around the Sun) using the angular momentum principle to update total angular momentum over the course of a certain amount of time. Initial constants were defined- such as the position of the Sun and comet, radii of the Sun and comet, mass of the Sun and comet, initial velocity of the comet, inertia of the comet (inertia for a sphere is equal to 2/5 times the mass of the comet times the radius of the comet squared), angular velocity of the comet about its own axis, force applied to the comet, and G (the gravitational constant). In the while loop, the momentum of the comet is found and the gravitational force of the Sun on the comet is found to update the position of the comet as it orbits the Sun. Next, translational momentum of the comet around the Sun is found by the cross product of the momentum of the comet and r (which is the distance from the comet to the Sun). Rotational angular momentum is found by multiplyng the inertia of the comet with the angular velocity of the comet. Total angular momentum is the sum of Lrot and Ltrans. Torque is found by the cross product of force and r and then torque is used to update the total angular momentum as the comet orbits the Sun. The code prints the final total angular momentum after the specified time t using the angular momentum principle to update angular momentum as the comet goes along its orbit.
Examples
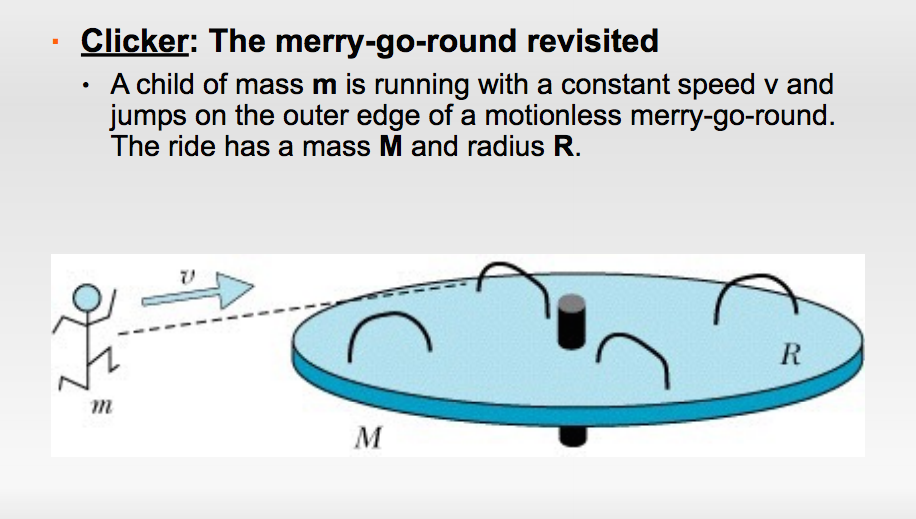
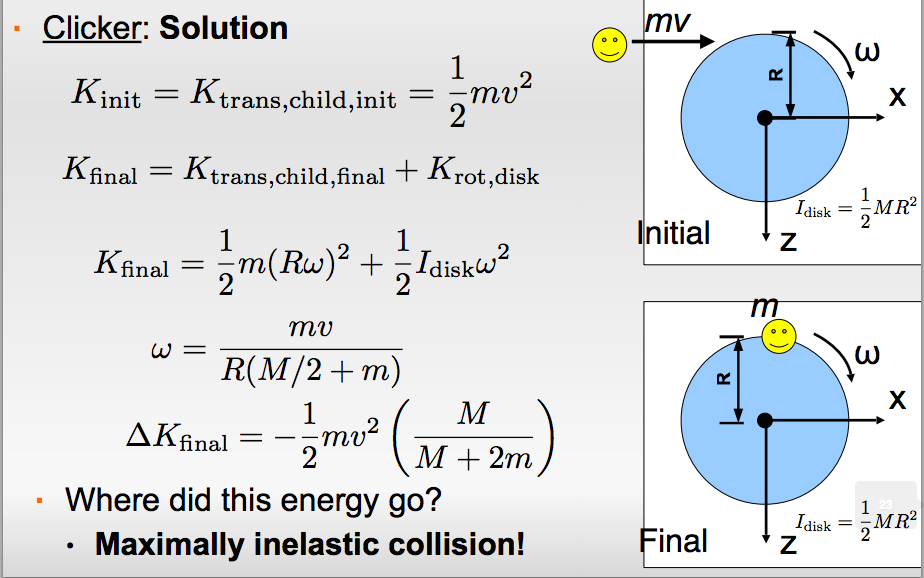
Simple
Middle
Difficult
Connectedness
How is this topic connected to something that you are interested in? How is it connected to your major? Is there an interesting industrial application?
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
Internet resources on this topic
References
This section contains the the references you used while writing this page