Franck-Hertz Experiment: Difference between revisions
Tbennett37 (talk | contribs) |
Tbennett37 (talk | contribs) No edit summary |
||
| Line 28: | Line 28: | ||
===Simple=== | ===Simple=== | ||
In this example, an electron has used all of its kinetic energy to excite a hydrogen atom from its | In this example, an electron has used all of its kinetic energy to excite a hydrogen atom from its first excited state to it’s second excited state. How much kinetic energy did the electron have? | ||
<math>E_{H*,f} = E_{H,i} + K_{e}</math> | <math>E_{H*,f} = E_{H,i} + K_{e}</math> | ||
| Line 34: | Line 34: | ||
Since hydrogen has an energy of -13.6 eV at it’s ground state, we know that the same equation is equal to: | Since hydrogen has an energy of -13.6 eV at it’s ground state, we know that the same equation is equal to: | ||
<math>{\frac{-13.6 eV}{ | <math>{\frac{-13.6 eV}{3^2}} = {\frac{-13.6 eV}{1^2}} + K_{e}</math> | ||
<math>K_{e} = | <math>K_{e} = 1.89 eV</math> | ||
===Middling=== | ===Middling=== | ||
Revision as of 09:25, 1 December 2015
Claimed and created by Tyler Bennett
Main Idea
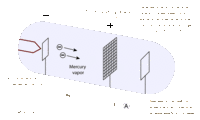
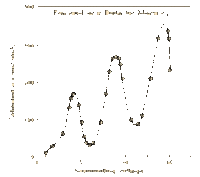
James Franck and Gustav Hertz were German physicists that helped to prove the Quantum Theory using their collisional excitation experiment in 1914. The quantum theory states that atoms have discrete levels made up of electrons of specific kinetic energies for each level. To confirm this, the Franck-Hertz duo created an accelerating apparatus, which simply sends electrons with varying kinetic energies through a vapor (in this case, mercury vapor) and then collects the electrons that weren’t picked up by the atoms using a collector. The results showed that once the electrons reached the threshold kinetic energy of 4.9 eV, most of them were picked up by the atoms, and they didn’t reach the collector [2]. This proved that the first level of the mercury atoms needs electrons with at least 4.9 eV to be absorbed. This technique was used with other elements to find their own threshold kinetic energies.
A Mathematical Model
where [math]\displaystyle{ E_{H*, f} }[/math] is the final energy of the atom plus the energy of the electrons and [math]\displaystyle{ K_{e, f} }[/math] is the final energy left over by the passing electrons. [math]\displaystyle{ E_{H, i} }[/math] and [math]\displaystyle{ K_{e,i} }[/math] are the initial quantities of the atom and the electron before the collision of the two or before the absorption of the photon. This equation is consistent with conservation of energy, meaning that there is no loss or gain of energy from outside of the system.
- For example [math]\displaystyle{ {\frac{d\vec{p}}{dt}}_{system} = \vec{F}_{net} }[/math] where p is the momentum of the system and F is the net force from the surroundings.
A Computational Model
This image is an accurate visualization of how electrons could jump to different levels or be "excited" to the next level. "n=1" is called the ground level, "n=2" is called the first excited state. "n=2" is called the second excited state, and so on.
This is another way to visualize the different quantizations of an atom. This graph in particular shows the different levels of energy with the change of "r" or distance from the proton.
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Simple
In this example, an electron has used all of its kinetic energy to excite a hydrogen atom from its first excited state to it’s second excited state. How much kinetic energy did the electron have?
[math]\displaystyle{ E_{H*,f} = E_{H,i} + K_{e} }[/math]
Since hydrogen has an energy of -13.6 eV at it’s ground state, we know that the same equation is equal to:
[math]\displaystyle{ {\frac{-13.6 eV}{3^2}} = {\frac{-13.6 eV}{1^2}} + K_{e} }[/math]
[math]\displaystyle{ K_{e} = 1.89 eV }[/math]
Middling
An electron has now use a partial amount of its kinetic energy to excite a hydrogen atom from its ground level to its third excited state. If you are given the initial kinetic energy of the electron, can you find out how much energy is left over?
[math]\displaystyle{ E_{H*,f} + K_{e,f} = E_{H,i} + K_{e, i} }[/math]
The electron begins with 12.8 eV.
[math]\displaystyle{ {\frac{-13.6 eV}{4^2}} + K_{e,f}= {\frac{-13.6 eV}{1^2}} + 12.8 eV }[/math]
[math]\displaystyle{ K_{e,f} = 0.05 eV }[/math]
Difficult
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
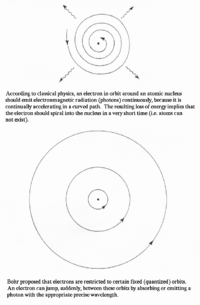
In 1911, Ernest Rutherford created a model of the atom which was proven wrong in the next couple of years. His model displayed only a single level that spiraled about the nucleus of the atom. Niels Bohr noted that this model would mean that atoms could not exist, as the electrons would spiral into the nucleus. Bohr then came up with his own model in 1913 that consisted of different shells outside of the atom. The electrons could jump shells and they would have constant quantized orbits. The Franck-Hertz experiment confirmed this model in showing that atoms can only obtain electrons when they contain enough kinetic energy to be able to jump onto the atoms’ shells.
See also
Further reading
Books, Articles or other print media on this topic
External links
Internet resources on this topic
References
[1] Chabay, Ruth W., and Bruce A. Sherwood. "Energy Quantization." Matter & Interactions. 3rd ed. Hoboken: Wiley, 2011. Print.
[2] Nave, R. "The Franck-Hertz Experiment." Hyper Physics. Hyper Physics. Web. 27 Nov. 2015.
[3] "Bohr Atomic Model." Bohr Atomic Model. Abyss. Web. 27 Nov. 2015.


