Specific Heat Capacity

by Dejan Tojcic

Specific Heat Capacity

Specific Heat Capacity is simply a physical quantity that represents the ratio of the amount of heat taken or added to substance or object which results in a temperature change. The formal definition of Specific Heat is the amount of heat required to raise the temperature of 1 gram of a substance 1°C. The Standard Unit(SI) of this quantity is, joule per celsius per kilogram or or [math]\displaystyle{ \mathrm{\tfrac{J}{°C*Kg}} }[/math]. Different objects/substances have different specific heat capacities because every object has a varying mass, molecular structure, and numbers of particles per unit mass specific, and since specific heat capacity is reliant on mass, every different object has a different specific heat capacity.

File:Different objects have different specific heats

A Mathematical Model

In order to find the Specific Heat Capacity of a substance, we use the equation:[math]\displaystyle{ \Delta E_{\mathrm{thermal}} = C * M * \Delta T }[/math], and rearrange it to get [math]\displaystyle{ C= \Delta E_{\mathrm{thermal}} /( M * \Delta T) . }[/math] where C is the Specific Heat Capacity with units of joules per celsius per kilogram or [math]\displaystyle{ \mathrm{\tfrac{J}{°C*Kg}} }[/math], M is the mass measured in kilograms or [math]\displaystyle{ \mathrm{kg} }[/math], [math]\displaystyle{ \Delta E_{\mathrm{thermal}} }[/math] represents the change in thermal energy measured by joules or [math]\displaystyle{ \mathrm{J} }[/math], and [math]\displaystyle{ \Delta T }[/math] represents change in temperature with units celsius or [math]\displaystyle{ \mathrm{°C.} }[/math]

A Computational Model

How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript

Simple Example

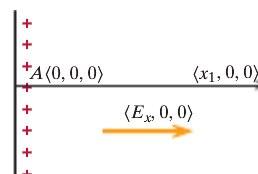
In this example, the electric field is equal to [math]\displaystyle{ E = \left(E_x, 0, 0\right) }[/math]. The initial location is A and the final location is C. In order to find the potential difference between A and C, we use [math]\displaystyle{ dV = V_C - V_A }[/math].

Since there are no y and z components of the electric field, the potential difference is [math]\displaystyle{ dV = -\left(E_x*\left(x_1 - 0\right) + 0*\left(-y_1 - 0\right) + 0*0\right) = -E_x*x_1 }[/math]

Let's say there is a location B at [math]\displaystyle{ \left(x_1, 0, 0\right) }[/math]. Now in order to find the potential difference between A and C, we need to find the potential difference between A and B and then between B and C.

The potential difference between A and B is [math]\displaystyle{ dV = V_B - V_A = -\left(E_x*\left(x_1 - 0\right) + 0*0 + 0*0\right) = -E_x*x_1 }[/math].

The potential difference between B and C is [math]\displaystyle{ dV = V_C - V_B = -\left(E_x*0 + 0*\left(-y_1 - 0\right) + 0*0\right) = 0 }[/math].

Therefore, the potential difference A and C is [math]\displaystyle{ V_C - V_A = \left(V_C - V_B\right) + \left(V_B - V_A\right) = E_x*x_1 }[/math], which is the same answer that we got when we did not use location B.

Connectedness

1. How is this topic connected to something that you are interested in?
2. How is it connected to your major?
3. Is there an interesting industrial application?

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

External links

Internet resources on this topic

References

This section contains the the references you used while writing this page