Point Particle Systems: Difference between revisions
Akerrison3 (talk | contribs) |
Akerrison3 (talk | contribs) |
||
| Line 48: | Line 48: | ||
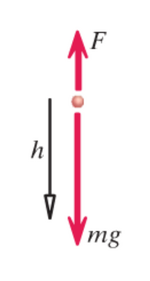
You pull up on a string the distance '''d''', 0.2 m, with a force, '''F''', 0.3 N. The yo-yo falls a distance '''h''', 0.35 m. What is the change in translational kinetic energy? | You pull up on a string the distance '''d''', 0.2 m, with a force, '''F''', 0.3 N. The yo-yo falls a distance '''h''', 0.35 m. What is the change in translational kinetic energy? | ||
[[File:Yo-yoo.png| | [[File:Yo-yoo.png|150 px]] | ||
===Spring in a Box Example=== | ===Spring in a Box Example=== | ||
Revision as of 14:57, 1 December 2015
This topic has been claimed akerrison3.
The Main Idea
The point particle method of measuring changes in energy simplifies the system of interest down to a single point, or focuses on its center of mass. Therefore, the only energy changing in the system is translational kinetic energy. Translational kinetic energy is the energy that comes from an object moving from one location to another. This can then be used in the extended system of the object, which includes all energy transfers.
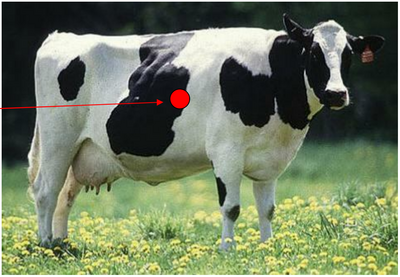 Center of Mass of a Cow as a Point
Center of Mass of a Cow as a Point
A Mathematical Model
Translational kinetic energy is equal to 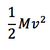 , where M is mass and v is the velocity of the center of mass.
, where M is mass and v is the velocity of the center of mass.
The change in translational kinetic energy is equal to ![]() , where F is the net force acting on the object and delta r is the change in position of the object center of mass.
, where F is the net force acting on the object and delta r is the change in position of the object center of mass.
In the point particle system, total change in energy is equal to the total change in kinetic energy. Because of the energy principle, ![]() , where delta E is change in total energy and W is work, the change in translational kinetic energy is equal to work. Remember, work is equal to
, where delta E is change in total energy and W is work, the change in translational kinetic energy is equal to work. Remember, work is equal to ![]() as well.
as well.
Examples
Jumper Model
A person jumps straight up in the air from a crouching position. Their center of mass moves h, or 2 meters. Their total mass, m is equal to 60 kg. Find the velocity of the center of mass of the jumper. When the jumper jumps, the normal force of the ground is equal to 2x the force of gravity.
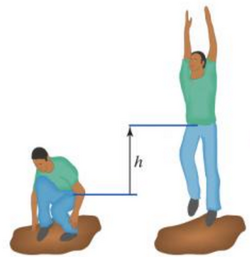
Imagine the jumper's center of mass as a point, and it moves up 2 meters.
Remember, ![]() and
and ![]() .
We need to find Fnet. The only forces acting on the jumper are the gravitational force of the Earth and the normal force. Therefore, Fnet = Fn-Fg.
Fg = Mg, therefore Fn = 2Mg.
.
We need to find Fnet. The only forces acting on the jumper are the gravitational force of the Earth and the normal force. Therefore, Fnet = Fn-Fg.
Fg = Mg, therefore Fn = 2Mg.
Steps:
When worked out, the v = 6.26 m/s.
The final translational kinetic energy can be used for further calculations if one was to calculate the total change in energy of the real system, including perhaps the thermal energy of the body when jumping increasing, or the rotational kinetic energy of the arms moving.
Yo-Yo Example
You pull up on a string the distance d, 0.2 m, with a force, F, 0.3 N. The yo-yo falls a distance h, 0.35 m. What is the change in translational kinetic energy?
Spring in a Box Example
Connectedness
- How is this topic connected to something that you are interested in?
I think it is interesting how physicists have simplified the process of finding changes of energy in a system in order to make approximations and calculate more complicated changes in energy. For me, it really helped me to understand exactly what translational kinetic energy is and how it applies to the entire system.
- How is it connected to your major?
My major is industrial engineering, and although I do not think this topic applies directly to my major, it applies to simplifying and making a more efficient and easy way to calculate the changes of energy in a system. That is the goal of industrial engineering, so in that way, I really enjoy this method of finding changes in energy.
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
Internet resources on this topic
References
Chabay, Ruth W., and Bruce A. Sherwood. "9." Matter & Interactions. N.p.: n.p., n.d. N. pag. Print.