Tension

claimed by Jae Hee Kim (chloejhkim)

This topic covers Tension.

What is Tension?

The tension force is the force that is transmitted through objects like string, rope, or wire when it is pulled tight by forces acting from opposite side. The tension force is directed along the length of the rope and pulls equally on the objects on the opposite side of the rope.

It's important to note that tension is only a pulling force since ropes simply can't push effectively or push by itself. Trying to push with a rope causes the rope to go slack and lose the tension that allowed it to pull in the first place. This might sound obvious, but when it comes time to draw the forces acting on an object, it is important to remember that tension can only pull on an object.

---

How To Calculate Tension Force

Use Newton's second law to relate the motion of the object to the forces.

1. Draw the forces exerted on the object in the question.
2. Write down Newton's second law (a= ​ΣF/m ) for a direction in which the tension is directed.
3. Solve for the tension using the Newton's second law equation (a= ​ΣF/m )

​​ Following these three steps will solve tension problem.

Example Problems

Example 1: Angled rope pulling on a box

A 2.0kg box of toy box t is being pulled across a table by a rope at an angle θ=60º as seen below (ignore friction). The tension in the rope causes the box to slide across the table to the right with an acceleration of 3.0 m/s^2

What is the tension in the rope?

First draw a force diagram of all the forces acting on the box.

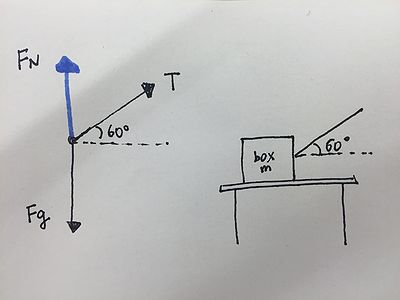
Now use Newton's second law. The tension is directed both vertically and horizontally, so it's a little unclear which direction to choose. However, since the acceleration is going horizontally, and since the tension is the only force directed horizontally, use Newton's second law in the horizontal direction.

1. a= ​ΣF/m (use Newtons's second law for the horizontal direction)
2. 3.0 m/s^2=Tcos60º/2.0kg ​​ (plug in the horizontal acceleration, mass, and horizontal forces)
3. Tcos60º=(3.0 m/s^2)(2.0kg)
4. T=[(3.0 m/s^2)(2.0kg)]/(cos60º)
5. T=12N

Example 2: Box hanging from two ropes

A 0.25 kg container hangs at rest from two strings secured to the ceiling and wall respectively. The diagonal rope under tension T1 is directed at an angle θ=30º from the horizontal direction as seen below.

What are the tensions (T1 and T2) in the two strings?

First draw a force diagram of all the forces acting on the container.

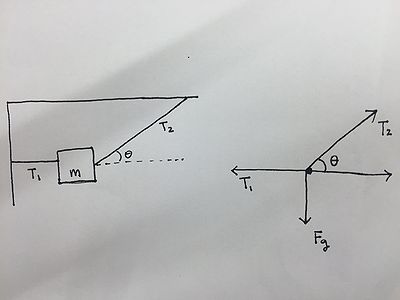
Now use Newton's second law. There are tensions directed both vertically and horizontally, so again it's a little unclear which direction to choose. However, since there is force of gravity (a vertical force), start with Newton's second law in the vertical direction.

1. a=​ΣF/m (use Newton's second law for the vertical direction)
2. 0=(T2*sin30º-Fg)/0.25kg
3. T2=Fg/(sin30º)
4. T2=mg/(sin30º)
5. T2=[(0.25kg)(9.8m/s²)]/(sin30º)
6. T2=4.9N

Now that we know T2 we can solve for the tension T1 using Newton's second law for the horizontal direction.

1. a=​ΣF/m (use Newtons's second law for the horizontal direction)
2. 0=(T2*cos30º-T1)/0.25kg (plug in the horizontal acceleration, mass, and horizontal forces)
3. T1=T2*cos30º
4. T1=(4.9N)*cos30º
5. T1=4.2N

​

Connectedness

1. How is this topic connected to something that you are interested in?

When I was little, I went to a department store and I saw a transparent elevator. I never knew how elevator operated but through the transparent elevator, I realized that the pulling force of the ropes was what was keeping the elevator moving. This pulling force is tension and I later realized that this tension force is evident in everywhere in my daily life.

1. How is it connected to your major?

I am not exactly sure how tension is connected to industrial engineering, which is my major. However, what I can say is that tension is a very basic concept in physics related to force and it is important to understand physics mechanism in studying industrial engineering.

1. Is there an interesting industrial application?

Tension force is applied in everyday life, just like the elevator example I mentioned. Tension force is applied when I pull a clothing tags.

See also

1. Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

I think it will be interesting to make connection between tension force and friction. Use both tension and friction in pulling a box in ice skating environment and concrete environment. This would be a good example to explore more about the topic.

Further reading

Books, Articles or other print media on this topic

Chabay, Ruth W., and Bruce A. Sherwood. Matter & Interactions. Hoboken, NJ: John Wiley & Sons, 2015. Print.

External links

Internet resources on this topic

References

This section contains the the references you used while writing this page

Chabay, Ruth W., and Bruce A. Sherwood. Matter & Interactions. Hoboken, NJ: John Wiley & Sons, 2015. Print. https://www.khanacademy.org/science/physics/forces-newtons-laws/tension-tutorial/a/what-is-tension http://www.physicsclassroom.com/Class/newtlaws/U2L2b.cfm#tension http://hyperphysics.phy-astr.gsu.edu/hbase/mlif.html http://hyperphysics.phy-astr.gsu.edu/hbase/elev.html http://www.softschools.com/formulas/physics/tension_formula/70/ http://physics.stackexchange.com/questions/36175/understanding-tension http://www.brightstorm.com/science/physics/newtons-laws-of-motion/tension/