Electric Dipole: Difference between revisions

From Physics Book
Jump to navigation Jump to search
Line 8: Line 8:
===An Exact Model===
===An Exact Model===
[[File:Dipole.png|300px|thumb|An Electric Dipole]]
[[File:Dipole.png|300px|thumb|An Electric Dipole]]
Since an electric dipole is made up of 2 electric point charges, the electric field of the dipole can be calculated by summing the electric fields contributed by each point charge.  In the example, the field at point P, <math>E_{P}</math> is equivalent to the sum of the electric field from the positive charge <math>q+</math> and the negative charge <math>q-</math>.
An electric dipole is constructed from two point charges, one at position <math>[\frac{d}{2}, 0]</math> and one at position <math>[\frac{-d}{2}, 0]</math>. These point charges are of equal and opposite charge. We then wish to know the electric field due to the dipole at some point <math>p</math> in the plane (see the figure). <math>p</math> can be considered either a distance <math>[x_0, y_0]</math> from the midpoint of the dipole, or a distance <math>r</math> and an angle <math>\theta</math> as in the diagram.
In other words, <math>E_{P} = E_{P_{q+}} + E_{P_{q-}}</math>.


Substituting in the equation for the electric field from a point charge we get <math>\vec E_{P} = \frac{1}{4\pi\epsilon_{0}} \times \frac{q_{+}}{|r_{+}|^{2}} \times \hat r_{+} + \frac{1}{4\pi\epsilon_{0}} \times \frac{q_{-}}{|r_{-}|^{2}} \times \hat r_{-}</math>.
Then we begin by calculating <math>r_+</math> and <math>r_-</math> the radii from the positive and negative particles to the point <math>p</math>. In this example, we will assume that the positive particle is closer to <math>p</math>, but its simple to modify this derivation for the opposite case. First, we divide <math>r</math> into its x and y components, <math> r_x = r * cos(\theta) </math> and <math> r_y = r * sin(\theta) </math>.
 
A simple refactoring gives <math>\vec E_{P} = \frac{1}{4\pi\epsilon_{0}} \times (\frac{q_{+}}{|r_{+}|^{2}}\hat r_{+} + \frac{q_{-}}{|r_{-}|^{2}} \hat r_{-})</math>.
 
Since <math>q_+ = -1 * q_-</math>, this is equivalent to <math>\vec E_{P} = \frac{q_+}{4\pi\epsilon_{0}} \times (\frac{\hat r_{+}}{|r_{+}|^{2}} - \frac{\hat r_{-}}{|r_{-}|^{2}})</math>
 
<math>|r_+| \text{ and } |r_-|</math> can then be calculated as <math>|r_+| = \sqrt{(|r_x| + \frac{d}{2})^2 + |r_y|^2}</math>, by decomposing <math>\vec r</math> into its components and factoring.
 
By a similar method, <math>|r_-| = \sqrt{(|r_x| - \frac{d}{2})^2 + |r_y|^2}</math>.
 
By substituting <math>|\vec r| \cos(\theta) \text{ and } |\vec r| \sin(\theta)</math> for  <math>|r_x| \text{ and } |r_y|</math> respectively, we get
 
<math>|r_+| = \sqrt{(|\vec r| \cos(\theta) + \frac{d}{2})^2 + (|\vec r| \sin(\theta))^2}</math> and <math>|r_-| = \sqrt{(|\vec r| \cos(\theta) - \frac{d}{2})^2 + (|\vec r| \sin(\theta))^2}</math>
 
We next expand the squared terms inside the radical: <math>\sqrt{(|\vec r| \cos(\theta))^2 + \frac{d |\vec r| \cos(\theta)}{2} + \frac{d^2}{4} +(|\vec r| \sin(\theta))^2}</math>
 
Rearranging, <math>\sqrt{|\vec r|^2 * (\cos(\theta)^2 + \sin(\theta)^2) + \frac{d |\vec r| \cos(\theta)}{2} + \frac{d^2}{4}} = \sqrt{|\vec r|^2 + \frac{d |\vec r| \cos(\theta)}{2} + \frac{d^2}{4}} = |r_+|</math>
 
By a similar method, <math>|r_-| = \sqrt{|\vec r|^2 - \frac{d |\vec r| \cos(\theta)}{2} + \frac{d^2}{4}}</math>
 
Plugging this into the earlier equation, we get the monstrosity <math>E_{P} = \frac{q_+}{4\pi\epsilon_{0}} \times (\frac{\hat r_{+}}{|\vec r|^2 + \frac{d |\vec r| \cos(\theta)}{2} + \frac{d^2}{4}} - \frac{\hat r_{-}}{|\vec r|^2 - \frac{d |\vec r| \cos(\theta)}{2} + \frac{d^2}{4}})</math>
 
To subtract the fractions, we first put them in like terms:
 
<math> \frac{\hat r_{+}}{|\vec r|^2 + \frac{d |\vec r| \cos(\theta)}{2} + \frac{d^2}{4}}
\times
\frac{|\vec r|^2 - \frac{d |\vec r| \cos(\theta)}{2} + \frac{d^2}{4}}{|\vec r|^2 - \frac{d |\vec r| \cos(\theta)}{2} + \frac{d^2}{4}})
=
\frac{\hat r_{+}\times (|\vec r|^2 - \frac{d |\vec r| \cos(\theta)}{2} + \frac{d^2}{4})}{|\vec r|^4 - \frac{|\vec r|^2 d |\vec r| \cos(\theta)}{2} + \frac{|\vec r|^2 d^2}{4} + \frac{|\vec r|^2 d |\vec r| \cos(\theta)}{2} - \frac{d^2 |\vec r|^2 \cos(\theta)^2}{4} + \frac{d^3|\vec r|cos(\theta)}{8} + \frac{|\vec r|^2 d^2}{4} - \frac{d^3|\vec r|cos(\theta)}{8} + \frac{d^4}{16}}</math>
 
Cancelling like terms simplifies this to
<math>\frac{\hat r_{+}\times (|\vec r|^2 - \frac{d |\vec r| \cos(\theta)}{2} + \frac{d^2}{4})}{|\vec r|^4 + \frac{|\vec r|^2 d^2}{2} -\frac{d^2 |\vec r|^2 \cos(\theta)^2}{4} + \frac{d^4}{16}}</math>


==Examples==
==Examples==

Revision as of 14:13, 3 December 2015

An Electric Dipole is a pair of equal and opposite Point Charges separated by a small distance.

claimed by Jmorton32 (talk) 02:52, 19 October 2015 (EDT)

Mathematical Models

An Exact Model

An Electric Dipole

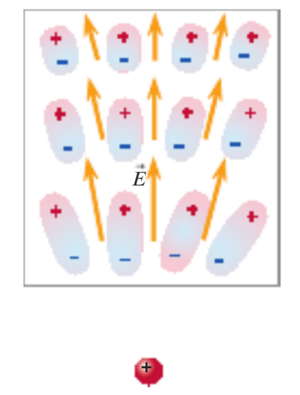
An electric dipole is constructed from two point charges, one at position [math]\displaystyle{ [\frac{d}{2}, 0] }[/math] and one at position [math]\displaystyle{ [\frac{-d}{2}, 0] }[/math]. These point charges are of equal and opposite charge. We then wish to know the electric field due to the dipole at some point [math]\displaystyle{ p }[/math] in the plane (see the figure). [math]\displaystyle{ p }[/math] can be considered either a distance [math]\displaystyle{ [x_0, y_0] }[/math] from the midpoint of the dipole, or a distance [math]\displaystyle{ r }[/math] and an angle [math]\displaystyle{ \theta }[/math] as in the diagram.

Then we begin by calculating [math]\displaystyle{ r_+ }[/math] and [math]\displaystyle{ r_- }[/math] the radii from the positive and negative particles to the point [math]\displaystyle{ p }[/math]. In this example, we will assume that the positive particle is closer to [math]\displaystyle{ p }[/math], but its simple to modify this derivation for the opposite case. First, we divide [math]\displaystyle{ r }[/math] into its x and y components, [math]\displaystyle{ r_x = r * cos(\theta) }[/math] and [math]\displaystyle{ r_y = r * sin(\theta) }[/math].

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

Middling

Difficult

Connectedness

  1. How is this topic connected to something that you are interested in?
  2. How is it connected to your major?
  3. Is there an interesting industrial application?

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

External links

Internet resources on this topic

References

This section contains the the references you used while writing this page

Retrieved from "http://www.physicsbook.gatech.edu/index.php?title=Electric_Dipole&oldid=10453"