Electric Dipole

An Electric Dipole is a pair of equal and opposite Point Charges separated by a small distance.

claimed by Jmorton32 (talk) 02:52, 19 October 2015 (EDT)

Mathematical Models

An Exact Model

An Electric Dipole

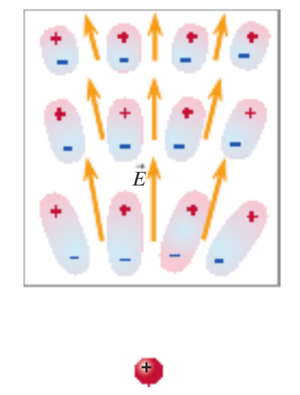
Since an electric dipole is made up of 2 electric point charges, the electric field of the dipole can be calculated by summing the electric fields contributed by each point charge. In the example, the field at point P, [math]\displaystyle{ E_{P} }[/math] is equivalent to the sum of the electric field from the positive charge [math]\displaystyle{ q+ }[/math] and the negative charge [math]\displaystyle{ q- }[/math]. In other words, [math]\displaystyle{ E_{P} = E_{P_{q+}} + E_{P_{q-}} }[/math].

Substituting in the equation for the electric field from a point charge we get [math]\displaystyle{ \vec E_{P} = \frac{1}{4\pi\epsilon_{0}} \times \frac{q_{+}}{|r_{+}|^{2}} \times \hat r_{+} + \frac{1}{4\pi\epsilon_{0}} \times \frac{q_{-}}{|r_{-}|^{2}} \times \hat r_{-} }[/math].

A simple refactoring gives [math]\displaystyle{ \vec E_{P} = \frac{1}{4\pi\epsilon_{0}} \times (\frac{q_{+}}{|r_{+}|^{2}}\hat r_{+} + \frac{q_{-}}{|r_{-}|^{2}} \hat r_{-}) }[/math].

Since [math]\displaystyle{ q_+ = -1 * q_- }[/math], this is equivalent to [math]\displaystyle{ \vec E_{P} = \frac{q_+}{4\pi\epsilon_{0}} \times (\frac{\hat r_{+}}{|r_{+}|^{2}} - \frac{\hat r_{-}}{|r_{-}|^{2}}) }[/math]

[math]\displaystyle{ |r_+| \text{ and } |r_-| }[/math] can then be calculated as [math]\displaystyle{ |r_+| = \sqrt{(|r_x| + \frac{d}{2})^2 + |r_y|^2} }[/math], by decomposing [math]\displaystyle{ \vec r }[/math] into its components and factoring.

By a similar method, [math]\displaystyle{ |r_-| = \sqrt{(|r_x| - \frac{d}{2})^2 + |r_y|^2} }[/math].

By substituting [math]\displaystyle{ |\vec r| \cos(\theta) \text{ and } |\vec r| \sin(\theta) }[/math] for [math]\displaystyle{ |r_x| \text{ and } |r_y| }[/math] respectively, we get

[math]\displaystyle{ |r_+| = \sqrt{(|\vec r| \cos(\theta) + \frac{d}{2})^2 + (|\vec r| \sin(\theta))^2} }[/math] and [math]\displaystyle{ |r_-| = \sqrt{(|\vec r| \cos(\theta) - \frac{d}{2})^2 + (|\vec r| \sin(\theta))^2} }[/math]

We next expand the squared terms inside the radical: [math]\displaystyle{ \sqrt{(|\vec r| \cos(\theta))^2 + \frac{d |\vec r| \cos(\theta)}{2} + \frac{d^2}{4} +(|\vec r| \sin(\theta))^2} }[/math]

Rearranging, [math]\displaystyle{ \sqrt{|\vec r|^2 * (\cos(\theta)^2 + \sin(\theta)^2) + \frac{d |\vec r| \cos(\theta)}{2} + \frac{d^2}{4}} = \sqrt{|\vec r|^2 + \frac{d |\vec r| \cos(\theta)}{2} + \frac{d^2}{4}} = |r_+| }[/math]

By a similar method, [math]\displaystyle{ |r_-| = \sqrt{|\vec r|^2 - \frac{d |\vec r| \cos(\theta)}{2} + \frac{d^2}{4}} }[/math]

Plugging this into the earlier equation, we get the monstrosity [math]\displaystyle{ E_{P} = \frac{q_+}{4\pi\epsilon_{0}} \times (\frac{\hat r_{+}}{|\vec r|^2 + \frac{d |\vec r| \cos(\theta)}{2} + \frac{d^2}{4}} - \frac{\hat r_{-}}{|\vec r|^2 - \frac{d |\vec r| \cos(\theta)}{2} + \frac{d^2}{4}}) }[/math]

To subtract the fractions, we first put them in like terms:

[math]\displaystyle{ \frac{\hat r_{+}}{|\vec r|^2 + \frac{d |\vec r| \cos(\theta)}{2} + \frac{d^2}{4}} \times \frac{|\vec r|^2 - \frac{d |\vec r| \cos(\theta)}{2} + \frac{d^2}{4}}{|\vec r|^2 - \frac{d |\vec r| \cos(\theta)}{2} + \frac{d^2}{4}}) = \frac{\hat r_{+}\times (|\vec r|^2 - \frac{d |\vec r| \cos(\theta)}{2} + \frac{d^2}{4})}{|\vec r|^4 - \frac{|\vec r|^2 d |\vec r| \cos(\theta)}{2} + \frac{|\vec r|^2 d^2}{4} + \frac{|\vec r|^2 d |\vec r| \cos(\theta)}{2} - \frac{d^2 |\vec r|^2 \cos(\theta)^2}{4} + \frac{d^3|\vec r|cos(\theta)}{8} + \frac{|\vec r|^2 d^2}{4} - \frac{d^3|\vec r|cos(\theta)}{8} + \frac{d^4}{16}} }[/math]

Cancelling like terms simplifies this to [math]\displaystyle{ \frac{\hat r_{+}\times (|\vec r|^2 - \frac{d |\vec r| \cos(\theta)}{2} + \frac{d^2}{4})}{|\vec r|^4 + \frac{|\vec r|^2 d^2}{2} -\frac{d^2 |\vec r|^2 \cos(\theta)^2}{4} + \frac{d^4}{16}} }[/math]

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Connectedness

1. How is this topic connected to something that you are interested in?
2. How is it connected to your major?
3. Is there an interesting industrial application?

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

External links

Internet resources on this topic

References

This section contains the the references you used while writing this page