Charged Disk

We will cover how to find the electric field of a uniformly charged disk, and how this can also apply to capacitors. (Shubham Shah)

The Main Idea

In this section, we will do a step-by-step process of calculating the electric field of a uniformly charged disk. This is especially important because two oppositely charged metal disks collectively are known as a capacitor, a concept seen in several places in physics and the real world.

A Mathematical Model

Before we begin our calculations, take a look at this image of a uniformly charged disk:

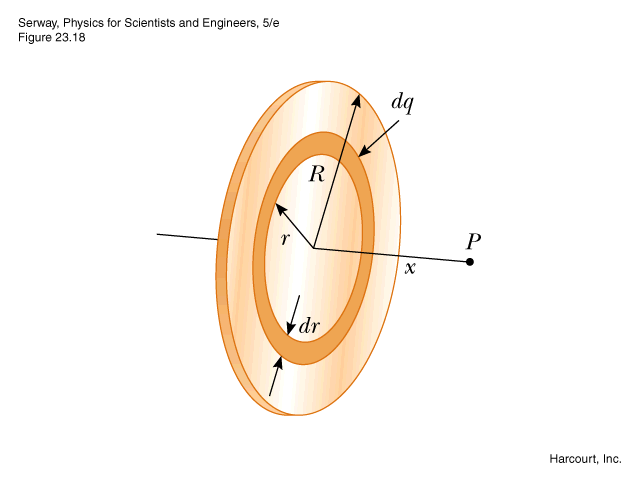
This image shows a visual representation of a disk. It should look pretty familiar. In fact, the shape of a disk is simply an extension of a ring. Think of it as infinitely many uniformly charged rings. Thinking of a disk this way will help to understand the equation of the electric field for a uniformly charged disk.

Recall the equation for the electric field of a uniformly charged ring:

[math]\displaystyle{ \ E= \frac{1}{4π\epsilon_0}\frac{qz}{sqrt((R^2+z^2)^3)} }[/math]

This equation will tell you the electric field of a uniformly charged ring at any observation location z. To apply this equation to a disk, integration will be involved. The integration variable in this case should be the radius of the ring [math]\displaystyle{ r }[/math], as that will change with the infinitely many concentric rings you have. However, [math]\displaystyle{ r }[/math] is nowhere to be found in the equation. But if the radius of each ring is different, what gets affected as a result?

[math]\displaystyle{ \ dq= Q\frac{2πrdr}{πr^2} }[/math]

Here you see that the charge of each ring is different due to the changing radius. The charge changes by a factor of the area of the ring, [math]\displaystyle{ 2πrdr }[/math], (if you roll out the ring, it is a rectangle with height [math]\displaystyle{ dr }[/math] and width [math]\displaystyle{ 2πr }[/math]) divided by the area of the disk, [math]\displaystyle{ πr^2 }[/math]. Plugging that in for the q variable in our integration, and then cancelling out some variables, will allow us to solve for the electric field of a disk:

[math]\displaystyle{ \ dE = \frac{1}{2\epsilon_0}\frac{Q}{πR^2}\frac{zrdr}{sqrt((R^2+z^2)^3)} }[/math]

Now we take the integral of this equation, and the result is this:

[math]\displaystyle{ \ E = \frac{1}{2\epsilon_0}\frac{Q}{πR^2}[1 - \frac{z}{sqrt(R^2+z^2)}] }[/math]

Thus, we have the equation that finds us the exact electric potential of a uniformly charged disk. You can still make approximations to make the formula simpler, however. If your observation location z is very close to the disk but not touching it, and is also significantly smaller than the radius of the disk (i.e. [math]\displaystyle{ 0 \lt \lt z \lt \lt R }[/math]), the equation becomes this:

[math]\displaystyle{ \ E = \frac{Q}{2\epsilon_0A} }[/math]

This is the most commonly seen form of this equation, and becomes very important when applied to the case of capacitors.

A Computational Model

How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Connectedness

1. How is this topic connected to something that you are interested in?
2. How is it connected to your major?
3. Is there an interesting industrial application?

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

External links

Internet resources on this topic

References

This section contains the the references you used while writing this page