Detecting a Magnetic Field: Difference between revisions
Ejohnston8 (talk | contribs) |
Ejohnston8 (talk | contribs) |
||
| Line 63: | Line 63: | ||
<math>{5.735e-6}={1e-7}{2I\over .003}</math> | <math>{5.735e-6}={1e-7}{2I\over .003}</math> | ||
<math>{{5.735e-6}*{.003}}\over{1e-7 *2}=I</math> | |||
<math>{{{5.735e-6}*{.003}}\over{1e-7 *2}}={I}</math> | |||
I=.086 A | |||
<math> B_{wire}={\mu_{0}\over4\pi}{2I\over d}</math> Now solve for the new <math>B_{wire}</math> given the current: I=.086 A and the new location d= .025m | |||
<math> B_{wire}={1e-7}{{2*.086}\over .025}</math> | |||
==Connectedness== | ==Connectedness== | ||
Revision as of 14:27, 22 November 2015
The Main Idea
A compass can be used to determine the magnetic field in a wire. If a compass is not in the proximity of any iron or steel object, the compass will naturally point in the direction of the Earth's magnetic north pole. If a current carrying wire is brought near the compass, the compass needle will deflect in the direction of the net magnetic field.
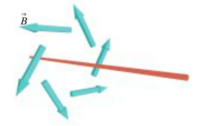
A Mathematical Model
A useful attribute of a compass is that you can calculate the the magnetic field of current carrying wire when you figure out the deflection angle. This equation is: [math]\displaystyle{ B_{wire}=B_{earth} tan(\theta) }[/math] where [math]\displaystyle{ \theta }[/math] is the deflection angle, [math]\displaystyle{ B_{earth} }[/math] is the earth's magnetic field which is a constant value of 2e-5 Tesla.
A Computational Model
<iframe width="420" height="315" src="https://www.youtube.com/embed/lwjk789NaVQ?rel=0" frameborder="0" allowfullscreen></iframe>
How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript
Examples
Simple
Problem 17.2.XP.003 from Matter and Interactions Book:
A current-carrying wire oriented north-south and laid over a compass deflects the compass 18° to the east. What is the magnitude of the magnetic field made by the current? The horizontal component of Earth's magnetic field is about [math]\displaystyle{ 2 ✕ 10^{-5} tesla }[/math] .
[math]\displaystyle{ B_{wire}=B_{earth} tan(\theta) }[/math]
[math]\displaystyle{ B_{wire}= 2 ✕ 10^{-5} tesla ✕ tan(18) }[/math]
[math]\displaystyle{ B_{wire}= 6.49✕ 10^{-6} Tesla }[/math]
What direction does the electron current flow in the wire?
The electron current flows from south to north.
Middling
Difficult
Problem 17.7.038 from Matter and Interactions Book:
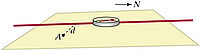
A long current-carrying wire, oriented North-South, lies on a table (it is connected to batteries which are not shown). A compass lies on top of the wire, with the compass needle about 3 mm above the wire. With the current running, the compass deflects 16 degrees to the West. At this location, the horizontal component of the Earth's magnetic field is about 2e-5 tesla.
What is the magnitude of the magnetic field at location A, on the table top, a distance 2.5 cm to the East of the wire, due only to the current in the wire?
[math]\displaystyle{ B_{wire}=B_{earth}tan(\theta) }[/math]
[math]\displaystyle{ B_{wire}=2e-5*tan(16) }[/math]
[math]\displaystyle{ B_{wire}=5.735e-6 T }[/math]
[math]\displaystyle{ B_{wire}={\mu_{0}\over4\pi}{2I\over r} }[/math] Where r is the distance the wire is from the compass.
Given: [math]\displaystyle{ B_{wire}=5.735e-6 }[/math] T, r= 0.003 m, and [math]\displaystyle{ {\mu_{0}\over4\pi}=1e-7; }[/math] Solve for the current :I
[math]\displaystyle{ {5.735e-6}={1e-7}{2I\over .003} }[/math]
[math]\displaystyle{ {{{5.735e-6}*{.003}}\over{1e-7 *2}}={I} }[/math]
I=.086 A
[math]\displaystyle{ B_{wire}={\mu_{0}\over4\pi}{2I\over d} }[/math] Now solve for the new [math]\displaystyle{ B_{wire} }[/math] given the current: I=.086 A and the new location d= .025m
[math]\displaystyle{ B_{wire}={1e-7}{{2*.086}\over .025} }[/math]
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History

This phenomenon was discovered by Danish scientist, Hans Oersted in 1826. After stumbling upon the deflection of a needle, he further investigated the math behind the event. He discovered that the magnitude of the magnetic field depends on the amount of current; if there is no current there will be no magnetic field. He also discovered that the deflection direction of the compass when the wire is above the wire is opposite the deflection direction when the wire is below the wire. This was the start of understanding magnetic fields.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
References
Chabay, R. & Sherwood, B. (2015). Matter and Interactions(4th Ed)(Vol 2). North Carolina: John Wiley & Sons,Inc.
Hans Christian Oersted. Digital image. MagCraft. National Imports, 2015. Web. 18 Nov. 2015. <http://www.rare-earth-magnets.com/hans-christian-oersted/>.