Direction of Magnetic Field

This page is here to provide an explanation for finding the direction of magnetic field. Since magnetic field is a cross product, finding its direction can be confusing at times, and you'll be asked many questions involving the direction of the magnetic field due to a moving charge, a current carrying wire, a current carrying coil, a bar magnet, etc. Hopefully this should work as a resource to come to when confused about anything regarding direction of magnetic fields!

The Main Idea

You previously learned about electric fields, and how a charged particle, or group of charged particles create a field in a specific pattern due to those particles' orientations. Magnetic field works in a similar fashion, but remember that it doesn't come from simply a charged particle, but a moving charged particle, with a velocity [math]\displaystyle{ \vec{v} }[/math]. Due to this new concept, we start to see some new patterns that you should want to get very familiar with.

A Mathematical Model

Recall that the equation for magnetic field due to a moving charged particle is [math]\displaystyle{ \vec{B} =\frac{\mu_0}{4\pi} \frac{(q\vec{v} \times \hat{r})}{|\vec{r}|^2} }[/math], otherwise known as the good-ole Biot-Savart law. The most important thing to note about this in regards to direction of magnetic field is that this is a cross product between the charge of the moving particle times its velocity, [math]\displaystyle{ q\vec{v} }[/math] and the unit distance vector from the particle to the observation location, [math]\displaystyle{ \hat{r} }[/math]. This Biot-Savart law is the basis for every orientation of magnetic field you will encounter in this class (wires, magnetic dipoles, etc), and its cross product is what makes finding the direction of magnetic field much trickier than finding the direction of electric field.

A Moving Charged Particle

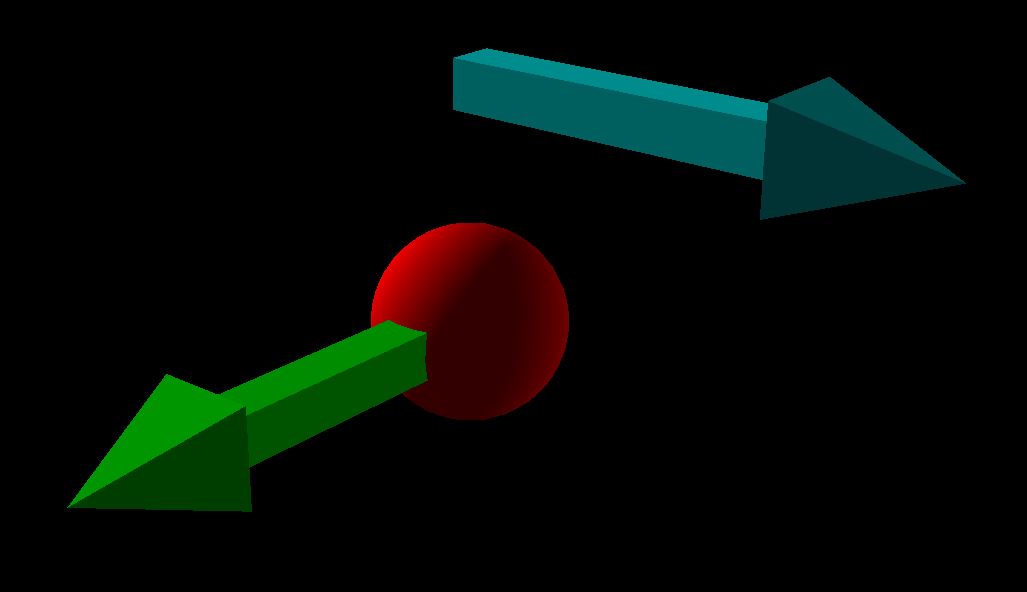
The first scenario you need to be familiar with is when a particle with a charge [math]\displaystyle{ q }[/math] has a velocity [math]\displaystyle{ v }[/math]. What does this look like? Check out the following image:

Imagine if the red particle was a proton and the green arrow was its velocity. In order to find the direction of the magnetic field created by the moving particle, you need to use the right hand rule, a commonly used tool for physics! The right hand rule appears whenever a cross product is used in a calculation.

Steps for right hand rule:

1. Point index finger in direction of first vector in the operation.
2. Point middle finger in direction of second vector in the operation.
3. Your thumb will naturally point in the direction of the cross product.

Here's a visual for you:

In our case, the cross product is [math]\displaystyle{ q\vec{v} \times \hat{r} }[/math]. So to find the direction of magnetic field for our proton, put your index finger in the direction of [math]\displaystyle{ q\vec{v} }[/math]. Then point your middle finger in the direction of [math]\displaystyle{ \hat{r} }[/math]. Your thumb should now naturally point in the direction of [math]\displaystyle{ \vec{B} }[/math]. Use the right hand rule for our proton, with an observation location above the proton. What do you get?

It should look something like this:

(Where the cyan arrow represents the direction of the magnetic field.)

Now what if our proton wasn't a proton, but an election? We now have a negatively charged particle, causing [math]\displaystyle{ q\vec{v} }[/math] to point in the opposite direction of [math]\displaystyle{ \vec{v} }[/math]. You'll need to adjust your right hand rule accordingly. Remember that you don't point your index finger in the direction of [math]\displaystyle{ \vec{v} }[/math] but in the direction of [math]\displaystyle{ q\vec{v} }[/math]. Using the right hand rule in this fashion, we come up with this:

Connectedness

1. How is this topic connected to something that you are interested in?
2. How is it connected to your major?
3. Is there an interesting industrial application?

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

External links

Internet resources on this topic

References

This section contains the the references you used while writing this page

Page initiated by --Dlong42 (talk) 23 October 2015