Vectors

Written by Elizabeth Robelo

The Main Idea

A vector is an object with a magnitude and a direction. The magnitude of a vector is a scalar. A vector is represented by an arrow. The length of the arrow is the vector’s magnitude and the direction the arrow points is its direction. The start of the arrow is called the tail. The end where the arrow head is located is called the head.

Vectors can be added and subtracted to each other. To add two vectors you put them head to tail. The connecting arrow starting from the tail of one to the head of the other is the new vector.

Adding vector A to B

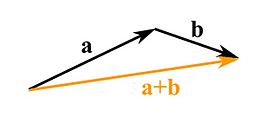
To subtract two vectors reverse the direction of the one you want to subtract and continue to add them like shown before.

Subtracting vector B from A

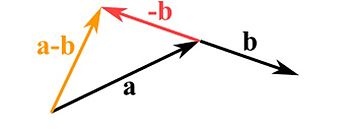
A unit vector is a vector that points in the same direction as the original vector with magnitude 1. We usually designate the unit vector with a "hat" [math]\displaystyle{ {\hat{\imath}} }[/math]. The unit vector is often called the normal vector.

A Mathematical Model

Vectors are given by x, y, and z coordinates. They are written in the form [math]\displaystyle{ A = \lt x, y, z\gt or xi + yj - zk. }[/math]

Magnitude: [math]\displaystyle{ |A| = \sqrt{x^2 + y^2 + z^2} }[/math]

Addition of two vectors: [math]\displaystyle{ {\lt a1, a2, a3\gt + \lt b1, b2, b3\gt } = {\lt a1 + b1, a2 + b2, a3 + b3\gt } }[/math]

Unit Vector: :[math]\displaystyle{ \mathbf{\hat{u}} = \frac{\mathbf{u}}{\|\mathbf{u}\|} }[/math]

A Computational Model

How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

Which of the following statements is correct?

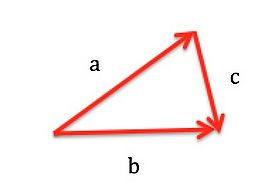
c = b + a a = b - c a = b + c b = a - c

[math]\displaystyle{ \overrightarrow{c}. = \overrightarrow{b}. + \overrightarrow{a}. }[/math]

Middling

What is the magnitude of the vector C = A - B if A = <6, 21, 17> and B = <12, 7, 15>?

Difficult

What is the unit vector in the direction of the vector <12, -15, 9>?

Connectedness

1. How is this topic connected to something that you are interested in?
2. How is it connected to your major?
3. Is there an interesting industrial application?

History

Giusto Bellavitis abstracted the basic idea of a vector in 1835 when he established the concept of equipollence. He called any pair of line segments of the same length and orientation equipollent. He found a relationship and created the first set of vectors.

The name vector was given to us by William Rowan Hamilton as part of his system of quaternions. The vectors he used were three dimensional.

Several other mathematicians developed similar vector systems to those of Bellavitis and Hamilton in the 19th century. The system used by Herman Grassman is the one that is most similar to the one used today. He thought of ideas similar to the cross product and vector differentiation.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

External links

[1]

References

This section contains the the references you used while writing this page