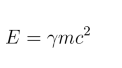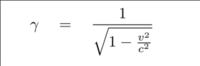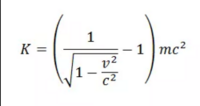Momentum at High Speeds: Difference between revisions
| Line 30: | Line 30: | ||
Lambda Alternate formulas are | Lambda Alternate formulas are | ||
[[File:Lambda_alternate_formulas.png|200px|thumb alt text]] | [[File:Lambda_alternate_formulas.png|200px|thumb alt text]] | ||
When we put this all together we get | |||
[[File:Without_lambda.png|200px|thumb alt text]] | |||
===A Computational Model=== | ===A Computational Model=== | ||
Revision as of 10:43, 4 December 2015
Momentum at High Speeds
By: Dalton Snyder
Short Description of Topic
The Main Idea
State, in your own words, the main idea for this topic Electric Field of Capacitor
A Mathematical Model
Momentum at High Speeds is an adaptation of Einstein's formula for Energy at rest
At Low velocities it is calculated using the formula
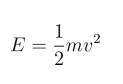
Einstein's Theory of Special Relativity
They found that when you approached the quantum level, the old formula for energy at rest did not apply so it was adapted to quantum mechanics.
This new adapted formula for energy at high speeds is:
The formula for Lambda is
Lambda Alternate formulas are
When we put this all together we get
A Computational Model
If you examine the formula for lambda, you will see that as the speed of the object approaches the speed of light, lambda becomes exponentially larger and larger. Thus as you approach light speed, a massive amount of Energy is needed and your momentum is huge. A good computer representation of this is:
Model: Lambda vs. Speed of Light Graph
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Simple
Middling
Difficult
References
http://scienceblogs.com/principles/2011/12/03/the-advent-calendar-of-physics-2/