Leon Foucalt: Difference between revisions

Revision as of 11:53, 4 December 2015

Claimed by Pierre

Leon Foucault

The Main Idea

Light passes through different materials, or mediums, at different speeds. In general, the denser the medium, the slower light passes through it. As light changes speed as it passes through a medium, it also bends at an angle. The optical density of a material is how well it can transmit light.

The Math of Refraction

The Index of Refraction: the ratio of the speed of light through a vacuum to the speed of light in the medium. Written as: [math]\displaystyle{ n=\frac{c}{v} }[/math], where
- c=speed of light in a vacuum
- v=speed of light in medium

Note that the index of refraction can never be less than one, since [math]\displaystyle{ \frac{c}{c}=1 }[/math].

Snell's Law: size of the angle of refraction, or how much the light bends. Written as:[math]\displaystyle{ n_1\sin\theta_1=n_2\sin\theta_2 }[/math], where
- [math]\displaystyle{ n_1 }[/math]=index of refraction of medium 1
- [math]\displaystyle{ n_2 }[/math]=index of refraction of medium 2
- [math]\displaystyle{ \theta_1 }[/math]=angle of incidence
- [math]\displaystyle{ \theta_2 }[/math]=angle of refraction.

A Visual Model

Here we see how the ray strikes a different medium and bends.

Here we see that the index of refraction is different for different wavelengths of light, so a prism will disperse white light.

Examples

Simple

Simple light from eye travels through water and bends:

Can be solved very easily with Snell's Law.

Middling

Single beam refraction through a prism with a laser pointer:

Calculations through a prism can be done as shown in the diagram below:

Difficult

While pretty, it is very difficult to solve for all the angles and indices of refraction correctly! This is how it works:

Connectedness

One of the most common uses of refraction is, quite simply, glasses. The way that light bends around a curved lens and refracts magnifies the image and can give you better eyesight.

On this vein, refractor telescopes, used in astronomy are quite common as well, especially among amateur astronomers.

Fiber optics is entirely dependent upon refraction and total internal reflection. These cables can send information at speeds approaching the speed of light, since the information is carried in the light itself.

Atmospheric refraction is also the cause of green flashes.

History

Thomas Harriot was the first person to discover that light bends when travelling through a different medium. However, it was Willebrord Snell who rediscovered it and then have the law of refraction named after him. It was initially published by Descartes in 1637, although Harriot had discovered it at least 35 years prior to that date.

Refractive lens began to be used on telescopes by 1608 and were the first type of optical telescopes developed.

References

https://en.wikipedia.org/wiki/Refracting_telescope

http://www-rohan.sdsu.edu/~aty/explain/optics/refr.html

@@ Line 1: / Line 1: @@
-Path Independence
+Claimed by Pierre
-(Redirected from Template)
-PLEASE DO NOT EDIT THIS PAGE. COPY THIS TEMPLATE AND PASTE IT INTO A NEW PAGE FOR YOUR TOPIC.
-Short Description of Topic
+Leon Foucault
-Contents [hide]
+==The Main Idea==
-The Main Idea
-.1 A Mathematical Model
-.2 A Computational Model
-Examples
-.1 Simple
-.2 Middling
-.3 Difficult
-Connectedness
-History
-See also
-.1 Further reading
-.2 External links
-References
-The Main Idea[edit]
-State, in your own words, the main idea for this topic
+Light passes through different materials, or mediums, at different speeds. In general, the denser the medium, the slower light passes through it. As light changes speed as it passes through a medium, it also bends at an angle. The <i>optical density</i> of a material is how well it can transmit light.
-A Mathematical Model[edit]
+===The Math of Refraction===
-What are the mathematical equations that allow us to model this topic. For example dp⃗ dtsystem=F⃗ net where p is the momentum of the system and F is the net force from the surroundings.
-A Computational Model[edit]
+*The Index of Refraction: the ratio of the speed of light through a vacuum to the speed of light in the medium. Written as: <math>n=\frac{c}{v}</math>, where
-How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript
+**c=speed of light in a vacuum
+**v=speed of light in medium
+Note that the index of refraction can never be less than one, since <math>\frac{c}{c}=1</math>.
+*Snell's Law: size of the angle of refraction, or how much the light bends. Written as:<math>n_1\sin\theta_1=n_2\sin\theta_2</math>, where
+**<math>n_1</math>=index of refraction of medium 1
+**<math>n_2</math>=index of refraction of medium 2
+**<math>\theta_1</math>=angle of incidence
+**<math>\theta_2</math>=angle of refraction.
-Examples[edit]
+===A Visual Model===
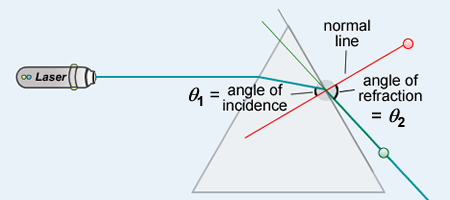
-Be sure to show all steps in your solution and include diagrams whenever possible
-Simple[edit]
+[[File:Refraction.png]]
-Middling[edit]
-Difficult[edit]
-Connectedness[edit]
-How is this topic connected to something that you are interested in?
-How is it connected to your major?
-Is there an interesting industrial application?
-History[edit]
-Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
-See also[edit]
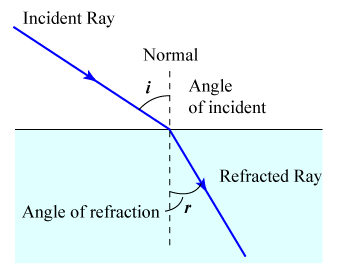
+Here we see how the ray strikes a different medium and bends.
-Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
-Further reading[edit]
-Books, Articles or other print media on this topic
-External links[edit]
-[1]
+[[File:Light_dispersion_conceptual_waves.gif ]]
-References[edit]
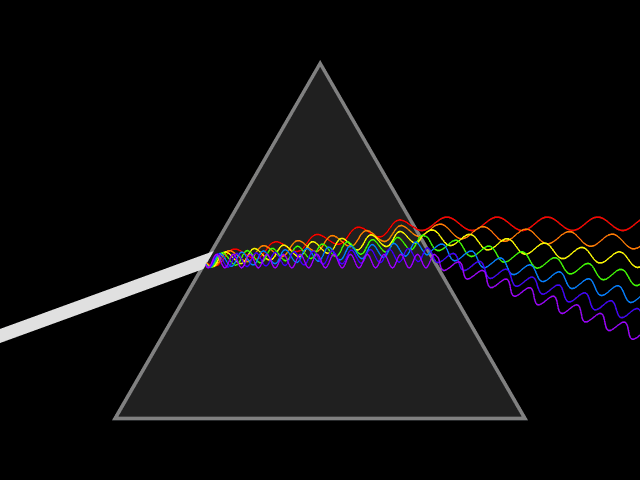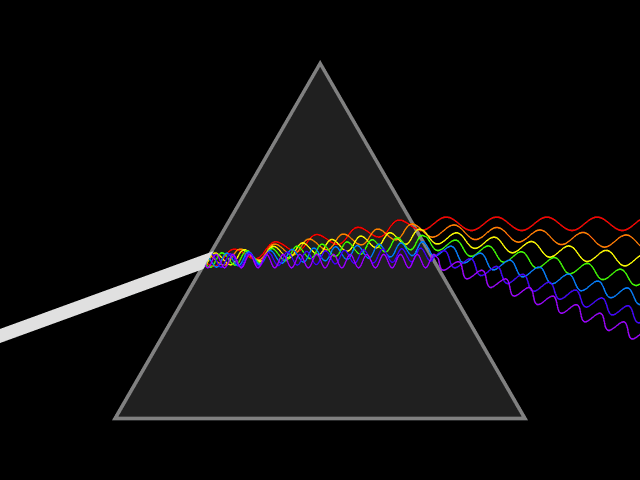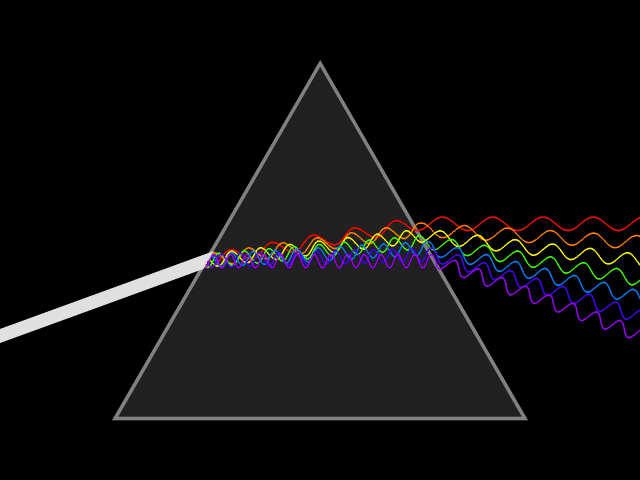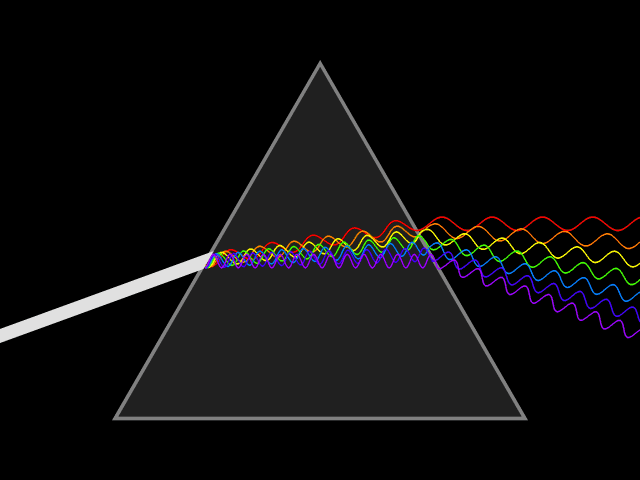
+Here we see that the index of refraction is different for different wavelengths of light, so a prism will disperse white light.
-This section contains the the references you used while writing this page
+==Examples==
+===Simple===
+Simple light from eye travels through water and bends:
+[[File:Refraction_fishbowl.jpg]]
+Can be solved very easily with Snell's Law.
+===Middling===
+Single beam refraction through a prism with a laser pointer:
+[[File:Laser1.jpg]]
+Calculations through a prism can be done as shown in the diagram below:
+[[File:Prismcalculations.png|400px]]
+===Difficult===
+[[File:Rainbow.jpg]]
+While pretty, it is very difficult to solve for all the angles and indices of refraction correctly!
+This is how it works:
+[[File:24-figure-48b.gif]]
+==Connectedness==
+One of the most common uses of refraction is, quite simply, glasses. The way that light bends around a curved lens and refracts magnifies the image and can give you better eyesight.
+On this vein, refractor telescopes, used in astronomy are quite common as well, especially among amateur astronomers.
+Fiber optics is entirely dependent upon refraction and total internal reflection. These cables can send information at speeds approaching the speed of light, since the information is carried in the light itself.
+Atmospheric refraction is also the cause of green flashes.
+==History==
+Thomas Harriot was the first person to discover that light bends when travelling through a different medium. However, it was Willebrord Snell who rediscovered it and then have the law of refraction named after him. It was initially published by Descartes in 1637, although Harriot had discovered it at least 35 years prior to that date.
+Refractive lens began to be used on telescopes by 1608 and were the first type of optical telescopes developed.
+== See also ==
+*[[Color Light Wave]]
+*[[Wave-Particle Duality]]
+===External links===
+http://www-rohan.sdsu.edu/~aty/explain/optics/refr.html
+http://ocw.mit.edu/courses/mechanical-engineering/2-71-optics-spring-2009/video-lectures/lecture-2-reflection-and-refraction-prisms-waveguides-and-dispersion/MIT2_71S09_lec02.pdf
+==References==
+https://en.wikipedia.org/wiki/Refracting_telescope
+http://www-rohan.sdsu.edu/~aty/explain/optics/refr.html
+[[Category:Optics]]