The Maxwell-Boltzmann Distribution: Difference between revisions
Sai95kamal (talk | contribs) |
Sai95kamal (talk | contribs) |
||
| Line 51: | Line 51: | ||
In addition, the graph below displays the effect of temperature on the distribution: | In addition, the graph below displays the effect of temperature on the distribution: | ||
[[File: maxbolts.jpg]] | [[File: maxbolts.jpg]] | ||
==Examples== | ==Examples== | ||
Revision as of 16:29, 4 December 2015
Claimed by Sai Srinivas
The Main Idea
In the context of the Kinetic Molecular Theory of Gases, a gas has a large number of particles moving around with varying speeds, colliding with each other, causing changes in the speeds and directions of the particles. A good understanding of the properties of a gas requires the knowledge of the distribution of particles speeds. Named after James Clerk Maxwell and Ludwig Boltzmann, the Maxwell-Boltzmann Distribution describes particles speeds in an idealized gas, in which the particles rarely interact with each other except for the brief collisions where energy and momentum are affected. The distribution of a particular gas depends on certain parameters, such as temperature of the system and mass of the gas particles. Certain properties of real gases inhibit their ability to be modeled by the Maxwell-Boltzmann Distribution so this distribution is best suited for application to ideal gases and certain rarefied gases at normal temperatures. Knowledge of particle speeds given by this distribution is important to scientists performing reactions because for a reaction to take place, particles must collide with sufficient energy to induce a transition state. This usually pertains to faster particles, so if the Maxwell-Boltzmann Distribution tells us how many particles have energies or speeds above a certain threshold, this is considered valuable information.
A Mathematical Model
The Maxwell–Boltzmann distribution is the function
- [math]\displaystyle{ f(v) = \sqrt{\left(\frac{m}{2 \pi kT}\right)^3}\, 4\pi v^2 e^{- \frac{mv^2}{2kT}}, }[/math]
where [math]\displaystyle{ m }[/math] is the particle mass and [math]\displaystyle{ kT }[/math] is the product of Boltzmann's constant, [math]\displaystyle{ k }[/math], and thermodynamic temperature, given by [math]\displaystyle{ T }[/math].
The probability that a molecule of a gas has a center-of-mass speed within the range [math]\displaystyle{ v }[/math] to [math]\displaystyle{ v+dv }[/math] is given by [math]\displaystyle{ f(v)dv }[/math].
As has been mentioned, the Maxwell-Boltzmann Distribution details the distribution of particle speeds in an ideal gas, and this distribution can be characterized in a few ways shown below:
- The average speed, [math]\displaystyle{ v_a }[/math], is the sum of the speeds of all particles divided by the number of particles in the volume of gas:
- [math]\displaystyle{ v_a = \int_0^{\infty} v \, f(v) \, dv= \sqrt { \frac{8kT}{\pi m}}= \sqrt { \frac{8RT}{\pi M}} }[/math]
where R is the gas constant and M is the molar mass of the substance.
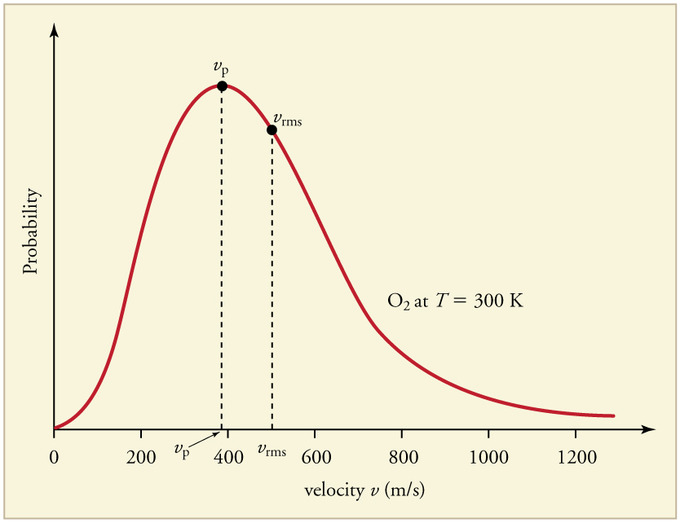
- The most probable speed, [math]\displaystyle{ v_p }[/math], is the speed associated with the highest point on the Maxwell-Boltzmann Distribution curve. Only a few particles will have this speed. To find this point on the distribution, we must calculate df/dv, set it equal to zero, and then solve for v. Then, we can ascertain:
- [math]\displaystyle{ v_p = \sqrt { \frac{2kT}{m} } = \sqrt { \frac{2RT}{M} } }[/math]
-The root-mean-square speed, [math]\displaystyle{ v_r }[/math], is the square root of the average speed-squared and is given by:
- [math]\displaystyle{ v_r = \left(\int_0^{\infty} v^2 \, f(v) \, dv \right)^{1/2}= \sqrt { \frac{3kT}{m}}= \sqrt { \frac{3RT}{M} } }[/math]
If a gas is in thermal equilibrium and follows the Maxwell-Boltzmann Distribution, the following relation always is discovered:
- [math]\displaystyle{ v_p \lt v_a \lt v_r }[/math]
A Computational Model
How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript
To visualize how a Maxwell-Boltzmann Distribution plot looks like, the link below provides a demonstration to see how temperature of the system affects the particle speeds.
Maxwell-Boltzmann Temperature Effect Demo
In addition, the graph below displays the effect of temperature on the distribution:
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Simple
Middling
Difficult
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
References
This section contains the the references you used while writing this page