Pendulum Motion: Difference between revisions
No edit summary |
|||
| Line 69: | Line 69: | ||
[[File:Mary10.jpg|1000px]] | [[File:Mary10.jpg|1000px]] | ||
==History== | |||
[[File: download.jpeg|thumb|]] | |||
The first to study the properties of the pendulum was Italian scientist Galileo Galilei around 1602 which was was recorded in an extant report of his research in a letter to Guido Ubaldo dal Monte from Padua. It was said by his biographer and student, Vincenzo Viviani, that the swinging motion of a chandelier in the Pisa cathedral was what initiated his interest in the topic around 1582. The isochronism states that is a period of the pendulum is approximately independent of the amplitude or width of the swing. Galileo discovered this crucial property which helped him figure out that makes pendulums useful timekeepers. From his research he determined that the period is independent of the mass and proportional to the square root of the length of the pendulum. In 1641 Galileo created a design for a pendulum clock and left it for his son Vincenzo to construct. The pendulum was the first harmonic oscillator used by man. | |||
==Connectedness== | ==Connectedness== | ||
| Line 74: | Line 79: | ||
As you see in the pendulum history and usage in time telling, the pendulum motion can be seen in our everyday life. As an architecture major, I have always been interested art and design. Different sculptures, installations, and art pieces can even be achieved throughout the application of a pendulum motion. Take a look [https://www.youtube.com/watch?v=3rigdgiHmnQ here] and [https://www.youtube.com/watch?v=9Ba-KNFEdfY here] and [https://www.youtube.com/watch?v=fk0OLIPZ3GE here] | As you see in the pendulum history and usage in time telling, the pendulum motion can be seen in our everyday life. As an architecture major, I have always been interested art and design. Different sculptures, installations, and art pieces can even be achieved throughout the application of a pendulum motion. Take a look [https://www.youtube.com/watch?v=3rigdgiHmnQ here] and [https://www.youtube.com/watch?v=9Ba-KNFEdfY here] and [https://www.youtube.com/watch?v=fk0OLIPZ3GE here] | ||
== See also == | == See also == | ||
Revision as of 19:12, 4 December 2015
--mbriatta3 (talk) 14:17, 3 December 2015 (EST)
The pendulum is a mass hanging from a string of negligible mass that is fixed to a point. The equilibrium position of the pendulum is the position when the string and mass hang vertically downward. When pulled back away from this equilibrium state, the string and mass will swing back and forth. If there is no friction or air resistance applied then the pendulum will swing forever.
The Main Idea
Properties of Pendulum Motion
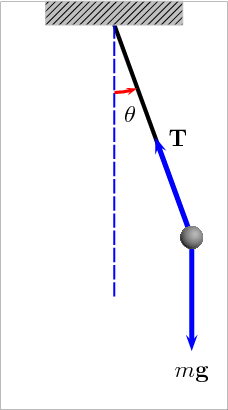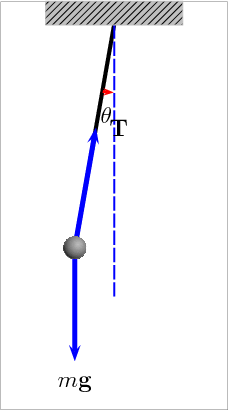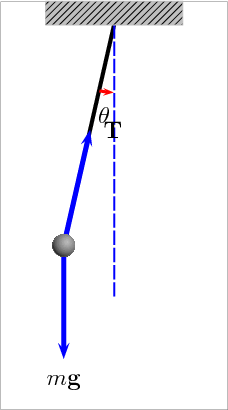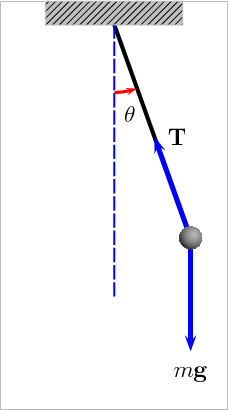
Animation of a pendulum showing forces acting on the mass: the tension T in the rod and the gravitational force mg. Link
A pendulum is just a mass hanging from a spring moving back and forth. In order to describe a pendulum, you need to understand its properties and parameters. There is a string with length L, a mass m hanging from the string, and it is pulled away from its equilibrium, there is an angle θmeasured off the vertical. The two forces acting on the pendulum when it is pulled away from its equilibrium are the string tension, Ft and the gravity, F = mg.
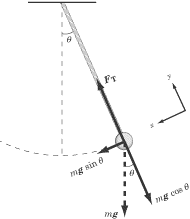
As long as the initial angle or amplitude of the swing is small, the major factor involved in the equations for calculating the frequency of a pendulum is the length of the rod or wire. Once you know the length of the pendulum, you can determine its frequency and speed.
Period of Oscillation
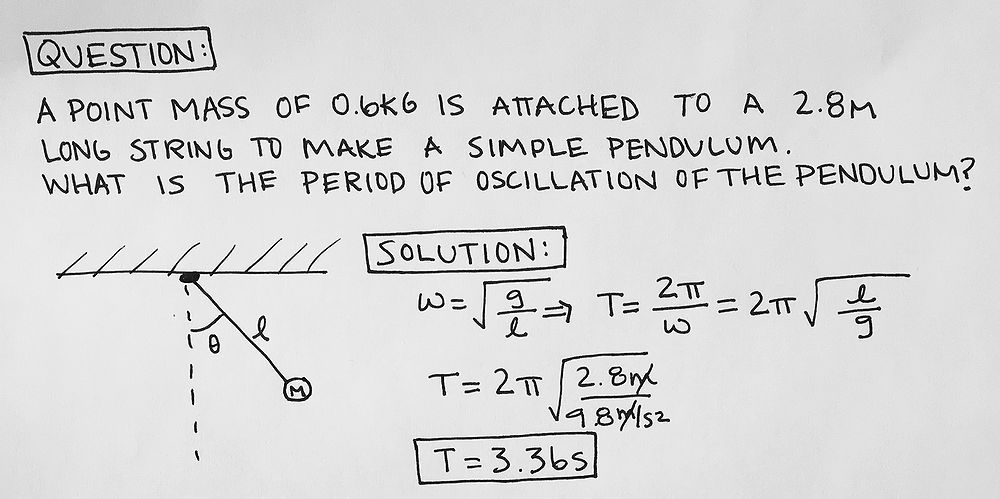
The period of oscillation of the pendulum, T, is defined in terms of the acceleration due to gravity, g, and the length of the pendulum, L, and to a small extent on the maximum angle that the pendulum swings away from vertical, θ0, called the amplitude
- [math]\displaystyle{ T \approx 2\pi \sqrt\frac{L}{g} \qquad \qquad \qquad \theta_0 \ll 1 \, }[/math]
This is a pretty scary-looking equation, but there’s really only one thing you need to gather from it: the longer the pendulum rope, the longer it will take for the pendulum to oscillate back and forth. You should also note that the mass of the pendulum bob and the angle of displacement play no role in determining the period of oscillation.
Energy
As long as there is no friction applied, mechanical energy in a pendulum is conserved. Total mechanical energy is a combination of gravitational potential energy kinetic energy. As the pendulum swings back and forth, there is a constant exchange between kinetic energy and gravitational potential energy. The potential energy of a pendulum, mgh, increases with the height of the weight as it swings. The image below shows that the potential energy is minimized at the equilibrium and is maximized at θ = ±θmax The kinetic energy and velocity of the pendulum are maximized at the equilibrium point and minimized when θ = ±θmax
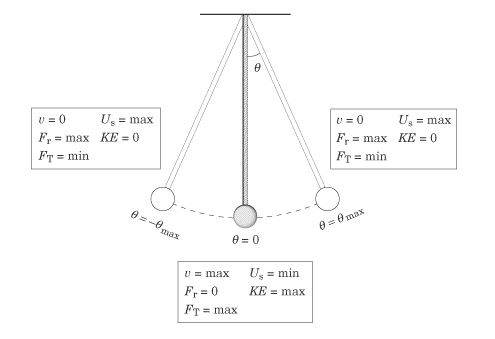
In the figure above, v is velocity, Fr is the restoring force, Ft is the tension in the pendulum string, Us is potential energy, and KE is kinetic energy.
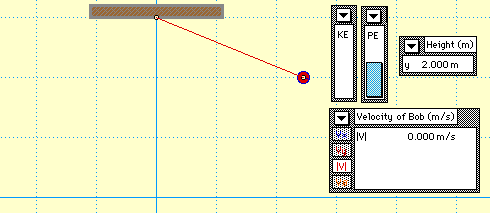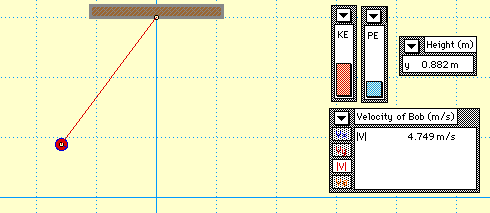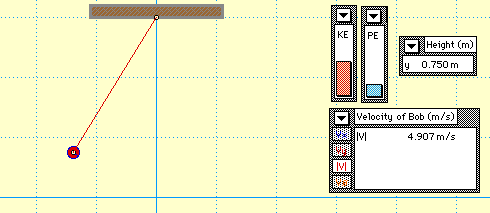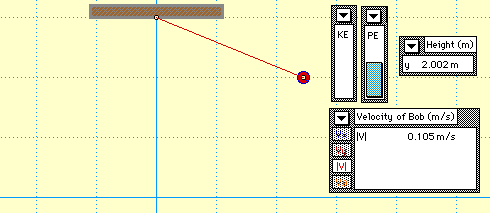
Velocity

The velocity can be approximated from the gravity equation for a weight dropping from a height.
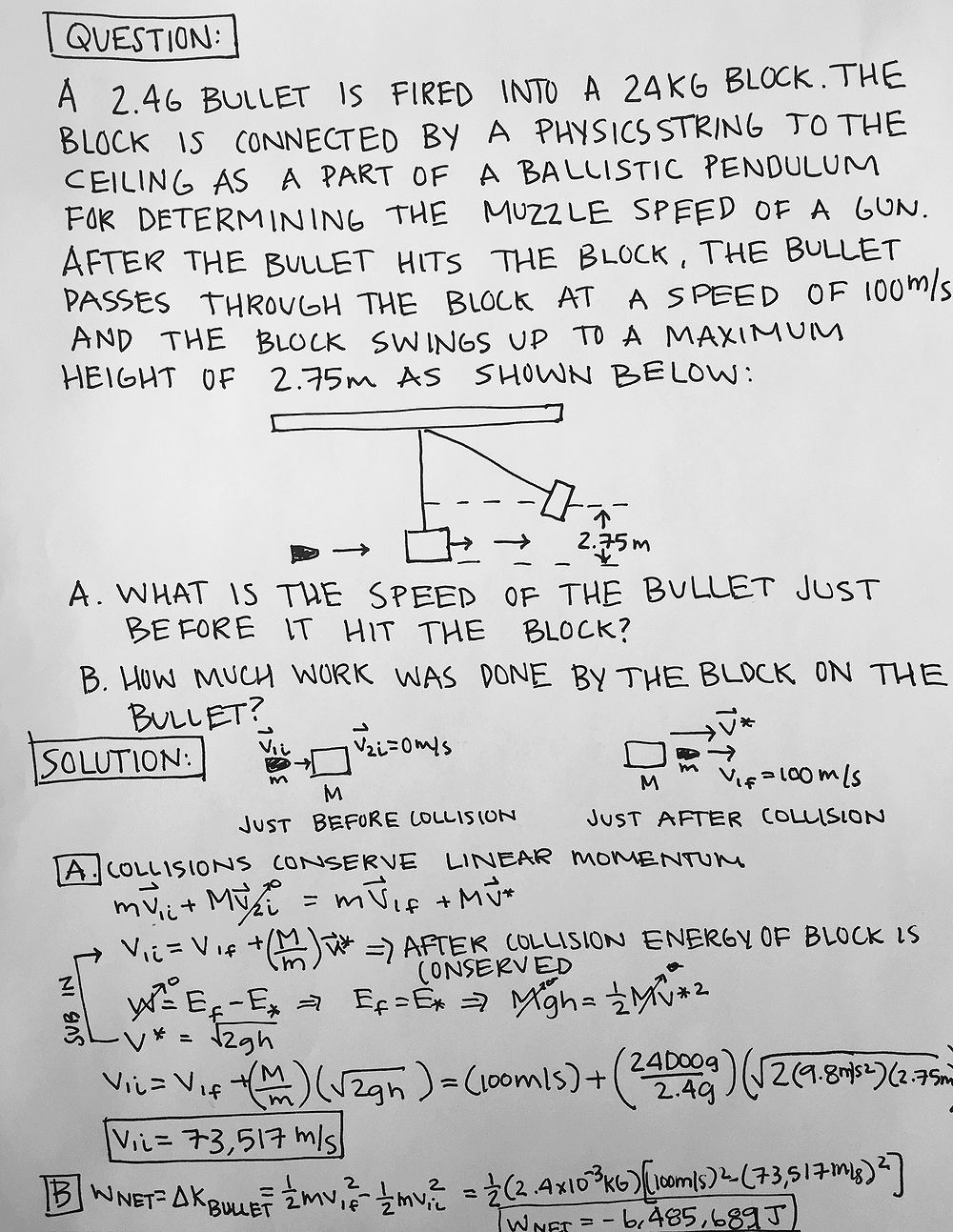
In order to calculate the the velocity of the pendulum mass at the equilibrium position, you have arrange the coordinate system so that the height of the mass at the equilibrium position is equal to zero. From this we can use the total mechanical energy which is equal to the kinetic energy at the equilibrium point where U = 0. This total mechanical energy also equals the total potential energy at where KE = 0. By putting these equations together we get:
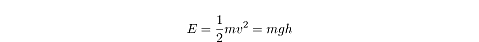
But what is height and how do we find it? The height is determined by the angle from the vertical that is the starting point of the pendulum's swing.
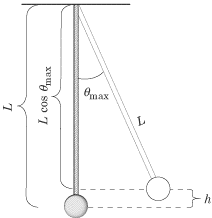
From the figure, we see that ![]() If we plug that value into the equation above, we can solve for v:
If we plug that value into the equation above, we can solve for v: 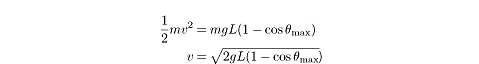
Examples
Simple
Middling
Difficult
History

The first to study the properties of the pendulum was Italian scientist Galileo Galilei around 1602 which was was recorded in an extant report of his research in a letter to Guido Ubaldo dal Monte from Padua. It was said by his biographer and student, Vincenzo Viviani, that the swinging motion of a chandelier in the Pisa cathedral was what initiated his interest in the topic around 1582. The isochronism states that is a period of the pendulum is approximately independent of the amplitude or width of the swing. Galileo discovered this crucial property which helped him figure out that makes pendulums useful timekeepers. From his research he determined that the period is independent of the mass and proportional to the square root of the length of the pendulum. In 1641 Galileo created a design for a pendulum clock and left it for his son Vincenzo to construct. The pendulum was the first harmonic oscillator used by man.
Connectedness

As you see in the pendulum history and usage in time telling, the pendulum motion can be seen in our everyday life. As an architecture major, I have always been interested art and design. Different sculptures, installations, and art pieces can even be achieved throughout the application of a pendulum motion. Take a look here and here and here
See also
- Barton's Pendulums
- Double Pendulum
- Pendulum Clock
- Pendulum (mathematics)
- Spherical Pendulum
- Simple Harmonic Motion
Further reading
- G. L. Baker and J. A. Blackburn (2009). The Pendulum: A Case Study in Physics (Oxford University Press).
- M. Gitterman (2010). The Chaotic Pendulum (World Scientific).
- Michael R. Matthews, Arthur Stinner, Colin F. Gauld (2005)The Pendulum: Scientific, Historical, Philosophical and Educational Perspectives, Springer
- Michael R. Matthews, Colin Gauld and Arthur Stinner (2005) The Pendulum: Its Place in Science, Culture and Pedagogy. Science & Education, 13, 261-277.
- Schlomo Silbermann,(2014) "Pendulum Fundamental; The Path Of Nowhere" (Book)
- Nelson, Robert; M. G. Olsson (February 1986). "The pendulum – Rich physics from a simple system". American Journal of Physics 54 (2): 112–121. Bibcode:1986AmJPh..54..112N. doi:10.1119/1.14703.
- L. P. Pook (2011). Understanding Pendulums: A Brief Introduction (Springer).
External links
References
- Chabay, Ruth W., and Bruce A. Sherwood. Matter and Interactions. Hoboken, NJ: Wiley, 2011. Print.
- "Pendulum Motion." Pendulum Motion. Physics Classroom, 1996. Web. 03 Dec. 2015.
- "Pendulum." Wikipedia. Wikimedia Foundation, n.d. Web. 03 Dec. 2015.