Lorentz Force

Claimed by Firas Sheikh--Fsheikh6 (talk) 21:09, 1 November 2015 (EST)

The Main Idea

The Lorentz Force is the combination of the Electric and Magnetic Forces. Basically the Lorentz Force is applied as a net force on a particle or number of particles when both electric and magnetic fields are present.

A Mathematical Model

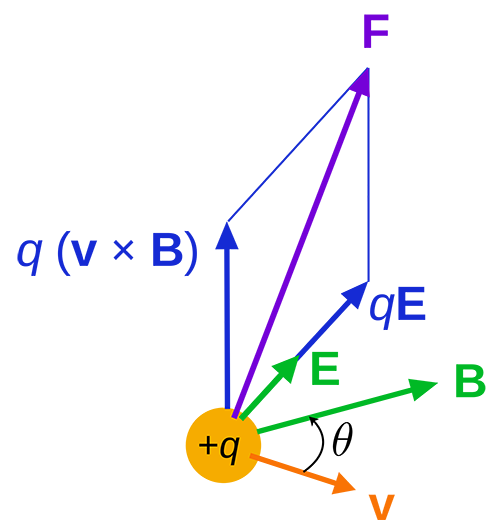
[math]\displaystyle{ \vec{F}_{Lorentz} = q\vec{E} + q\vec{v} ⨯ \vec{B} }[/math] where qE is the electric force and qv x B is the magnetic force.

A Computational Model

Examples

Be sure to show all steps in your solution and include diagrams whenever possible

Simple

The magnitude of the Electric Force at a certain point in space is 3e-9 and the magnitude of the Magnetic Force at that same point is -7e-9. What is the Lorentz Force at this point in space?

Force Lorenz = 3e-9 - 7e-9 = -4e-9 Newtons.

Middling

Find the Lorentz Force on an electron given that the magnitude of the Electric Field at a point in space is 4e-6 N/C and the magnitude of the magnetic field at that same point is 8e-7 T and the speed of the electron is 6000 m/s.

Force Electric = qE =(-1.6e-19)*(4e-6) = -6.4e-25 N Force Magnetic = q*B*v =(-1.6e-19)*(8e-7)(6000) = -7.68e-22 N Force Lorentz = Force Electric + Force Magnetic = -7.69 e-22 N

Difficult

An electron is 4e-9 m away from another electron. The magnetic field in the region is 4e3 T and the velocity of the electron is 40000 m/s. What is the Lorentz force on the electron.

Electric Force = (9e9)((1.6e-19*1.6e-19)/((4e-9)^2)) = 1.44e-11 N Magnetic Force = (1.6e-19)*(4e3*40000) = 2.56 e-11 N Lorentz Force = 2.56e-11 +1.44e-11 = 4e-11 N

Connectedness

1. This is connected to physics 2 because it combines the electric and magnetic forces.
2. This applies to my major mostly because it is related to electric forces.

History

J.J. Thomson first found the correct formula. However, because of some errors and an imperfect description of the displacement current he was not credited with the discovery of this force. Oliver Heaviside fixed Thompson’s mistakes and found the correct form of the magnetic force on a moving charged object. Finally, in 1892, Hendrik Lorentz found the modern form of the formula for the electromagnetic force.

See also

Electric Field and Force. Magnetic Field and Force.

Further reading

Matter and Interactions Volume 2.

External links

Link for picture: https://upload.wikimedia.org/wikipedia/commons/thumb/7/7c/Lorentz_force_particle.svg/2000px-Lorentz_force_particle.svg.png

References

This section contains the the references you used while writing this page