Electromagnetic Spectrum: Difference between revisions
Croberts65 (talk | contribs) No edit summary |
Croberts65 (talk | contribs) No edit summary |
||
| Line 28: | Line 28: | ||
==Examples== | ==Examples== | ||
===Simple=== | ===Simple=== | ||
Calculate the frequency of violet light (450 nm). | Calculate the frequency of violet light (450 nm). | ||
1. <math> | 1. <math>v = {\frac{c}{\lambda}}</math> | ||
2. <math> | 2. <math>450 \times 10^{-9} = \frac {2.998 \times 10^8}{\lambda}</math> | ||
3. <math>\lambda = 6.662 \times 10^{14}</math> Hz | 3. <math>\frac {1}{\lambda} = \frac {450 \times 10^{-9}}{2.998 \times 10^8} = 1.501 \times 10^{-15}</math> | ||
4. <math>\lambda = 6.662 \times 10^{14}</math> Hz | |||
===Difficult=== | ===Difficult=== | ||
A small laser used as a pointer produces a beam of red light 2 mm in diameter, and has a power output of 4 milliwatts. What is the magnitude of the electric field in the laser beam? | A small laser used as a pointer produces a beam of red light 2 mm in diameter, and has a power output of 4 milliwatts. What is the magnitude of the electric field in the laser beam? | ||
1. <math>E = \sqrt { \frac{(4 \times 10^{-3}) / ((2/2) \pi \times 10^{-3 + -3})}{(2.998 \times 10^{8}) \times (8.85 \times 10^{-12})} }</math> | 1. <math>E = \sqrt {\frac{P/A}{c \times \epsilon_{0}}}</math> | ||
2. <math>E = \sqrt { \frac{(4 \times 10^{-3}) / ((2/2) \pi \times 10^{-3 + -3})}{(2.998 \times 10^{8}) \times (8.85 \times 10^{-12})} }</math> | |||
3. <math>E = \sqrt { \frac{4 \times 10^{3}}{2.65 \pi \times 10^{-3}} }</math> | |||
4. <math>E = \sqrt {4.80 \times 10^5} = 6.93 \times 10^{2}</math> | |||
==Interaction With Matter== | |||
{|class="wikitable" style="margin: 1em auto 1em auto; width:70%; font-size:95%; | |||
|+Electromagnetic radiation interaction with matter | |||
|- style="text-align:center; background:#BBB;" | |||
|- | |||
! Region of the spectrum | |||
! Main interactions with matter | |||
|- | |||
|[[Radio wave|Radio]] | |||
|Collective oscillation of charge carriers in bulk material ([[plasma oscillation]]). An example would be the oscillatory travels of the electrons in an [[antenna (radio)|antenna]]. | |||
|- | |||
|nowrap|[[Microwave]] through far [[infrared]] | |||
|Plasma oscillation, molecular rotation | |||
|- | |||
|Near [[infrared]] | |||
|Molecular vibration, plasma oscillation (in metals only) | |||
|- | |||
|[[Light|Visible]] | |||
|Molecular electron excitation (including pigment molecules found in the human retina), plasma oscillations (in metals only) | |||
|- | |||
|[[Ultraviolet]] | |||
|Excitation of molecular and atomic valence electrons, including ejection of the electrons ([[photoelectric effect]]) | |||
|- | |||
|[[Xray|X-rays]] | |||
|Excitation and ejection of core atomic electrons, [[Compton scattering]] (for low atomic numbers) | |||
|- | |||
|[[Gamma ray]]s | |||
|Energetic ejection of core electrons in heavy elements, [[Compton scattering]] (for all atomic numbers), excitation of atomic nuclei, including dissociation of nuclei | |||
|- | |||
|nowrap|High-energy [[gamma ray]]s | |||
|Creation of [[Virtual pair|particle-antiparticle pairs]]. At very high energies a single photon can create a shower of high-energy particles and antiparticles upon interaction with matter. | |||
|} | |||
==History== | ==History== | ||
| Line 54: | Line 90: | ||
==Connectedness== | ==Connectedness== | ||
The electromagnetic spectrum is used for a variety of things including | |||
*Cooking (microwaves) | *Cooking (microwaves) | ||
*Radio and Communication | *Radio and Communication | ||
| Line 62: | Line 98: | ||
*Medical Treatments (gamma rays, x-rays) | *Medical Treatments (gamma rays, x-rays) | ||
*Nuclear Physics | *Nuclear Physics | ||
*The sense of sight | |||
==References & Further Reading== | ==References & Further Reading== | ||
Revision as of 02:06, 5 December 2015
This page has been created and claimed by Clayton Roberts (Croberts65)
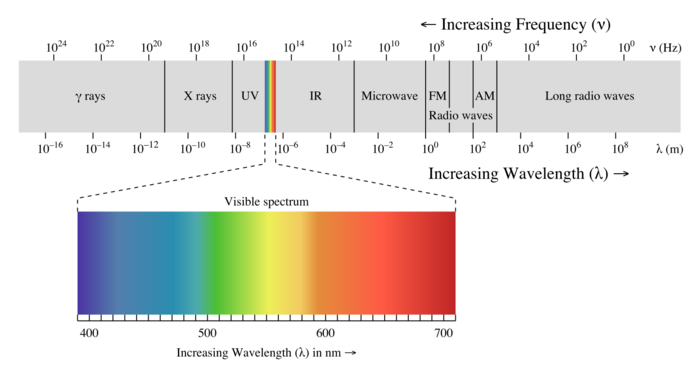
The electromagnetic spectrum describes all different frequencies of light that can be observed, and is most commonly associated with the visible chromatic colors.
The Main Idea
The frequency in Hertz (Hz) of electromagnetic waves can be related to the energy and color (if applicable) of the type of electromagnetic radiation. This can be used in chemistry for ionization, among other fields of science where the material and relative temperature can be related.
A Mathematical Model
[math]\displaystyle{ v = {\frac{c}{\lambda}} }[/math] where
- [math]\displaystyle{ v }[/math] is the frequency of the electromagnetic wave in Hertz (Hz) or number of cycles a second and can also be written as "[math]\displaystyle{ f }[/math]"
- [math]\displaystyle{ c }[/math] is the speed of light ( [math]\displaystyle{ 2.998 \times 10^8 \frac{m}{s} }[/math] )
- [math]\displaystyle{ \lambda }[/math] is the wavelength in meters
[math]\displaystyle{ E = \sqrt {\frac{P/A}{c \times \epsilon_{0}}} }[/math] where
- [math]\displaystyle{ E }[/math] is the magnitude of the electric field in Newtons per Columb (N/C)
- [math]\displaystyle{ P }[/math] is the power output of the beam of electromagnetic waves in Watts (W)
- [math]\displaystyle{ A }[/math] is the area of the beam in meters squared ( [math]\displaystyle{ m^{2} }[/math] )
- [math]\displaystyle{ \epsilon_{0} }[/math] is the vacuum permittivity constant ( [math]\displaystyle{ 8.85 \times 10^{-12} }[/math] )
- [math]\displaystyle{ c }[/math] is the speed of light ( [math]\displaystyle{ 2.998 \times 10^8 \frac{m}{s} }[/math] )
A Visual Model
Examples
Simple
Calculate the frequency of violet light (450 nm).
1. [math]\displaystyle{ v = {\frac{c}{\lambda}} }[/math]
2. [math]\displaystyle{ 450 \times 10^{-9} = \frac {2.998 \times 10^8}{\lambda} }[/math]
3. [math]\displaystyle{ \frac {1}{\lambda} = \frac {450 \times 10^{-9}}{2.998 \times 10^8} = 1.501 \times 10^{-15} }[/math]
4. [math]\displaystyle{ \lambda = 6.662 \times 10^{14} }[/math] Hz
Difficult
A small laser used as a pointer produces a beam of red light 2 mm in diameter, and has a power output of 4 milliwatts. What is the magnitude of the electric field in the laser beam?
1. [math]\displaystyle{ E = \sqrt {\frac{P/A}{c \times \epsilon_{0}}} }[/math]
2. [math]\displaystyle{ E = \sqrt { \frac{(4 \times 10^{-3}) / ((2/2) \pi \times 10^{-3 + -3})}{(2.998 \times 10^{8}) \times (8.85 \times 10^{-12})} } }[/math]
3. [math]\displaystyle{ E = \sqrt { \frac{4 \times 10^{3}}{2.65 \pi \times 10^{-3}} } }[/math]
4. [math]\displaystyle{ E = \sqrt {4.80 \times 10^5} = 6.93 \times 10^{2} }[/math]
Interaction With Matter
| Region of the spectrum | Main interactions with matter |
|---|---|
| Radio | Collective oscillation of charge carriers in bulk material (plasma oscillation). An example would be the oscillatory travels of the electrons in an antenna. |
| Microwave through far infrared | Plasma oscillation, molecular rotation |
| Near infrared | Molecular vibration, plasma oscillation (in metals only) |
| Visible | Molecular electron excitation (including pigment molecules found in the human retina), plasma oscillations (in metals only) |
| Ultraviolet | Excitation of molecular and atomic valence electrons, including ejection of the electrons (photoelectric effect) |
| X-rays | Excitation and ejection of core atomic electrons, Compton scattering (for low atomic numbers) |
| Gamma rays | Energetic ejection of core electrons in heavy elements, Compton scattering (for all atomic numbers), excitation of atomic nuclei, including dissociation of nuclei |
| High-energy gamma rays | Creation of particle-antiparticle pairs. At very high energies a single photon can create a shower of high-energy particles and antiparticles upon interaction with matter. |
History
The first time that a part of the electromagnetic spectrum was observed was in 1800, when scientist William Herschel was looking at light from a heated object through a prism. He noticed that the light surpassed the color red, into what we now know today as the infrared frequency of light. Some years later in 1845, Micheal Faraday made the connection between light and electromagnetism, when he observed that polarized light responded to a magnet. James Maxwell made the final step, when he realized that electromagnetic waves must travel at the speed of light.
Connectedness
The electromagnetic spectrum is used for a variety of things including
- Cooking (microwaves)
- Radio and Communication
- Radar
- Military Defense
- Environmental Impacts (ultraviolet light)
- Medical Treatments (gamma rays, x-rays)
- Nuclear Physics
- The sense of sight