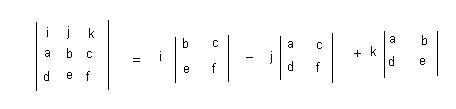Right Hand Rule

This topic covers Right Hand Rule. Claimed by: Layla Darian

The Main Idea

The magnitude of the translational angular momentum doesn't tell us everything about the motion of an object. For example, to describe the motion of Earth's orbit if you are standing on the positive z axis looking toward the origin, the Earth is moving counterclockwise in the xy plane. However, this statement cannot be used mathematically. You can't add "counterclockwise in the xy plane" to "clockwise in the yz plane." Instead, we can use the right hand rule to describe the direction of angular momentum as a vector. The direction can be specified like this:

• The plane in which both the position vector from the two objects and the momentum vector for the object of interest lie can be indicated by a unit vector perpendicular to that plane.
• The direction of motion within the plane (clockwise or counterclockwise) can be indicated by establishing a right hand rule (RHR) for this unit vector.
• Right Hand Rule: Using your right arm, point your arm to represent the "r" vector. Now turn your palm in the direction of the momentum vector. Curl your fingers in that direction of the momentum, and extend your thumb outward. The unit vector representing the direction of the angular momentum is defined to point in the direction of your thumb.
• Hint: If the rotational motion is counterclockwise, your right thumb, therefore the unit vector, will point out of the plane. If the rotational motion is clockwise, the unit vector will point into the plane.

A Mathematical Model

The direction of the angular momentum can also be solved through calculating the cross product of the r and p vectors.

The cross product of two vectors can be solved as so:

The first row is the standard basis vectors and must appear in the order given here. The second row is the components of r and the third row is the components of p. First, the terms alternate in sign and notice that the 2x2 is missing the column below the standard basis vector that multiplies it as well as the row of standard basis vectors. To solve for the "i" component, you use the expression: bf - ce. Do the same for the "j" and "k" components, and this will give you your vector. Your vector should be <bf-ce, af-cd, ae-bd>.

For more on the explanation of how to calculate cross product, visit this website: [1]

Here are some example problems. Try solving the cross product:

Click for the answer

Examples

Ans: 4

Ans: 4

Ans: 3

Connectedness

Right Hand Rule is essential for solving all angular momentum problems. Angular Momentum has been my favorite topic so far this semester. I think the problems and situations are very interesting, and they explain the reason behind why a lot of stuff in real life happen that we don't generally think about.

History

Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

External links

Internet resources on this topic

References

This section contains the the references you used while writing this page