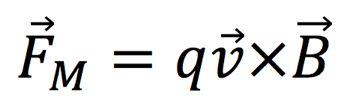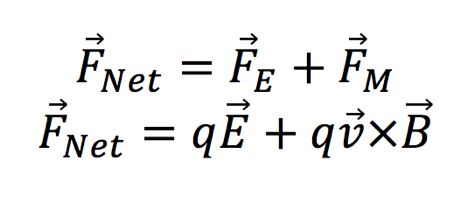Combining Electric and Magnetic Forces

Claimed by Alana Kaplan

Summary

When a charged particle is moving through a space with present electric and magnetic forces, if the forces are not balanced, the particles trajectory will change. It is important to remember that though the forces, observably, interact with a particle in different patterns, their effects can be quantitatively be compared.

Electric Forces

Qualitative

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Figure 1. An electric force acts in a pattern parallel to the electric field, pointing radially inward or outward of a particle. The direction depends on the signs of the interacting charged particles.

• A particle being acted upon by an electric force will move in a straight line, in the path, or negative path depending on charge, of the the electric field line (See Figure 1) .

• Electric fields point in a direction radially outward/ inward of a charged particle. There are four possible scenarios for the interaction of 2 charged particles:

1) A (-) charged Particle(1) is acting on a (-) charged particle(2)

• Particle(2) feels force pointing radially outward from Particle(1)

2) A (+) charged Particle(1) is acting on a (-) charged particle(2)

• Particle(2) feels force pointing radially inward toward Particle(1)

3) A (-) charged Particle(1) is acting on a (+) charged particle(2)

• Particle(2) feels force pointing radially inward toward Particle(1)

4) A (+) charged Particle(1) is acting on a (+) charged particle(2)

• Particle(2) feels force pointing radially outward from Particle(1)

Quantitative

The electric force formula is as follows:

Where 1 is the electric field from the source and 2 is the charge of the particle feeling the source

• Note that electric forces can perform work

Magnetic Forces

Figure 2. Magnetic Fields follow a helical pattern

Error creating thumbnail: sh: /usr/bin/convert: No such file or directory Error code: 127

Figure 3. Magnetic Force Right Hand Rule

Qualitative

• The magnetic force on a charged particle is orthogonal to the magnetic field.

• The particle must be moving with some velocity for a magnetic force to be present.

• Particles move perpendicular to the magnetic field lines in a helical manner (See Figure 2)

• To find the magnetic force, you can use the Right Hand Rule as follows (See Figure 3):

1) Thumb in direction of the velocity

2)Fingers in the direction of the magnetic field

3) Your palm will face in the direction of the Magnetic Force

Quantitative

The magnetic force on an object is:

Note that if the velocity and magnetic field are parallel the magnetic force is zero.

Electric and Magnetic Forces Combined

The net force acting on a particle passing through a magnetic and electric field is:

This net force calculation is known as "Lorentz Force"

When the net force is equal to zero, the velocity stays constant. The net force is equal when:

As seen in Figure 4 , when the net forces acting on a particle are balanced the electric field, magnetic field, and velocity vector are all perpendicular to each other. The electric and magnetic forces are equal but opposite.