Loop Rule: Difference between revisions
| Line 92: | Line 92: | ||
<math> {I}_{2}{R}_{2} - Q/C = 0 </math> | <math> {I}_{2}{R}_{2} - Q/C = 0 </math> | ||
From here, we can then solve for the current passing through a,b,d and e. We also know that the current passing through | From here, we can then solve for the current passing through a,b,d and e. We also know that the current passing through | ||
these points must be the same so <math> {I}_{1} = {I}_{2} </math> | these points must be the same so <math> {I}_{1} = {I}_{2} </math> | ||
| Line 103: | Line 102: | ||
So the current at a,b,d,e = <math> emf/({R}_{1} + {R}_{2}) </math> | So the current at a,b,d,e = <math> emf/({R}_{1} + {R}_{2}) </math> | ||
You must also know that once a capacitor is charging for a long time, current no longer flows through the capacitor. We can then | |||
easily solve for c because since current is no longer flowing through the capacitor, the current at c = 0. | |||
==History== | ==History== | ||
Revision as of 16:10, 5 December 2015
The Loop Rule is a fundamental principle of electric circuits that claims that in any round trip path in a circuit, Electric Potential equals zero.
Loop Rule
The loop rule simply states that in any round trip path in a circuit, Electric Potential equals zero. Keep in mind that this applies through ANY round trip path; there can be multiple round trip paths through more complex circuits. This principle deals with the conservation of energy within a circuit. Loop Rule and Node Rule are the two fundamental principle of electric circuits and are used to determine the behaviors of electric circuits. This principle is often used to solve for resistance of the light bulbs or other types of resistors or the current passing through these resistors.
A Mathematical Model
A mathematical representation is: [math]\displaystyle{ \Delta {V}_{1} + \Delta {V}_{2} + \space.... = 0 }[/math]
This can also be represented in a circuit as [math]\displaystyle{ emf = \Delta {V}_{1} + \Delta {V}_{2} + \space..... }[/math]
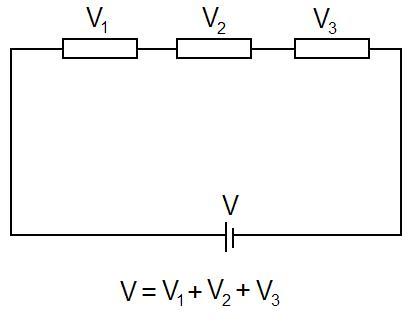
A Visual Model
The total voltage in the circuit is equal to all the individual voltages in the circuit added together.
Another way to think about it is [math]\displaystyle{ \Delta {V} - (\Delta {V}_{1} + \Delta {V}_{2} + \Delta {V}_{3})= 0 }[/math]
Examples
Simple
The circuit shown above consists of a single battery and a single resistor. The resistance of the wires is negligible for this problem.
Problem:
If the [math]\displaystyle{ emf }[/math] is 5 V and the resistance of the resistor is 10 ohms, what is the current passing through the resistor.
Solution:
Although we can solve this using the V = IR equation for the whole loop, lets examine this problem using the loop rule equation.
The loop rule equation would be [math]\displaystyle{ {V}_{battery} - {V}_{resistor} = 0 }[/math]
Since we know the [math]\displaystyle{ emf }[/math] of the battery we just need to find the potential difference through the resistor. For this we can use the equation of V = IR.
Thus we now have an loop rule equation of [math]\displaystyle{ emf - IR = 0 }[/math] From here it is a relatively simple process to find the current. We can rewrite the loop rule equation as [math]\displaystyle{ emf = IR }[/math] and then plug in 5 for the emf and 10 for the resistance, leaving us with I = .5 amperes.
Middling
Problem:
The circuit shown above consists of a single battery, whose [math]\displaystyle{ emf }[/math] is 1.3 V, and three wires made of the same material, but having different cross-sectional areas. Let the length of the thin wires be [math]\displaystyle{ {L}_{thick} }[/math] and the length of the thin wire be [math]\displaystyle{ {L}_{thin} }[/math] Find a loop rule equation that starts at the negative end of the battery and goes counterclockwise through the circuit.
Solution:
When beginning this problem, you must notice that the difference in cross-sectional areas affects the electric field in each wire. Because of this we will denote the electric field at D. as [math]\displaystyle{ {E}_{D} }[/math] and the electric field everywhere else as [math]\displaystyle{ {E}_{A} }[/math]. To begin we will go around the circuit clockwise and add up each component. First, we know that the [math]\displaystyle{ emf }[/math] of the battery is 1.3 V. Then, we will add up the potential voltage of each of the wires.
Remember that the electric potential of a wire is equal to the electric field * length of the wire. From his we can now find the potential difference of each section of the wires. The electric potential of location A - C is [math]\displaystyle{ {E}_{A} * {L}_{thick} }[/math]. This is the same for the electric potential of location E - G of the wire. For the thin section of the wire, the electric potential is [math]\displaystyle{ {E}_{D} * {L}_{thin} }[/math]. From here we just go around the circuit counterclockwise and add each potential difference to the loop rule equation.
Thus we can find that a loop rule equation is: [math]\displaystyle{ emf - 2 ({E}_{A} * {L}_{thick}) - {E}_{D} * {L}_{thin} = 0 }[/math]
This can also be rewritten as: [math]\displaystyle{ emf = 2 ({E}_{A} * {L}_{thick}) + {E}_{D} * {L}_{thin} = 0 }[/math]
Difficult
Problem:
For the circuit above, imagine a situation where the switch has been closed for a long time. Calculate the current at a,b,c,d,e and charge Q of the capacitor. Answer these using [math]\displaystyle{ emf, {R}_{1}, {R}_{2}, and \space C }[/math]
Solution:
First, write loop rule equations for each of the possible loops in the circuit. There are 3 loops that are possible.
[math]\displaystyle{ emf - {I}_{1}{R}_{1} - {I}_{2}{R}_{2} = 0 }[/math]
[math]\displaystyle{ emf - {I}_{1}{R}_{1} - Q/C = 0 }[/math]
[math]\displaystyle{ {I}_{2}{R}_{2} - Q/C = 0 }[/math]
From here, we can then solve for the current passing through a,b,d and e. We also know that the current passing through these points must be the same so [math]\displaystyle{ {I}_{1} = {I}_{2} }[/math]
[math]\displaystyle{ emf - {I}_{1}{R}_{1} - {I}_{1}{R}_{2} = 0 }[/math]
[math]\displaystyle{ emf = {I}_{1}({R}_{1} + {R}_{2}) = 0 }[/math]
[math]\displaystyle{ emf/({R}_{1} + {R}_{2}) = {I}_{1} }[/math]
So the current at a,b,d,e = [math]\displaystyle{ emf/({R}_{1} + {R}_{2}) }[/math]
You must also know that once a capacitor is charging for a long time, current no longer flows through the capacitor. We can then
easily solve for c because since current is no longer flowing through the capacitor, the current at c = 0.
History
The Loop Rule is formally known as the Kirchhoff Circuit Law, named after Gustav Kirchhoff discovered and defined this fundamental concept of electric circuits. He discovered this during his time as a student at Albertus University of Königsberg in 1845. Kirchoff went on to explore the topics of spectroscopy and black body radiation after his graduation from Albertus. Nowadays, it is used very often in electrical engineering. For more in depth information about Gustav Kirchhoff, visit the full wiki page on him: Gustav Kirchhoff

Connectedness
Because I am a Computer Science majors, while circuits are not directly connected to programming, computers and other electronics are made of different circuits. I assume that the Loop Rule is used in the electrical engineering that is required to create the circuits for the computers I use to program.
- Is there an interesting industrial application?
Since the Loop Rule is a fundamental principle of circuits, is it
See also
Other Circuit Concepts you can check out :
More Information and External links
Kirchoff's Circuit Laws - Wikipedia
Loop Rule - Boundless.com Textbook
Loop Rule - Doc Physics Video Lecture
References
- https://en.wikipedia.org/wiki/Kirchhoff%27s_circuit_laws#Kirchhoff.27s_voltage_law
- Chabay, Ruth W. Matter and Interactions: Electric and Magnetic Interactions. John Wiley, 2015. Print.
- http://www.ux1.eiu.edu/~cfadd/1360/28DC/Loop.html
Claimed by Bmock7