Charge Density: Difference between revisions
Zmatthews3 (talk | contribs) |
Zmatthews3 (talk | contribs) |
||
| Line 49: | Line 49: | ||
Volume charge density for the rod: <math>\rho = \frac{Q}{pi*R^{2}} </math> | Volume charge density for the rod: <math>\rho = \frac{Q}{pi*R^{2}} </math> | ||
Volume of infinitesimal portion: <math> pi*R^{2} \cdot dz </math> | |||
===Difficult=== | ===Difficult=== | ||
Revision as of 18:58, 5 December 2015
Created and Claimed by Zachary Matthews
The Main Idea
When considering the derivation of the electric field for objects extending the complexity of point charges, the concept of charge density is one that repeatedly makes an appearance. Essentially, this refers to the amount of charge per given measurement of space. Thus, because it can exist in one dimensional, two dimensional, and three dimensional forms, charge density can be represented as linear charge density, surface charge density, or volumetric charge density.
For an introductory physics course, the concept of charge density is especially useful because it allows us to come up with an expression for the charge density of an infinitesimal portion of a charge distribution, which we can then use for integration over the entirety of the object in finding the overall magnetic field.
A Mathematical Model
For each of the different types of charge density, the mathematical basis is the same, and it is quite obvious that each of the following can be related to the other two.
1) Linear charge density refers to the total amount of charge per unit length. It is modeled by the following equation:
[math]\displaystyle{ \lambda = \frac{Q}{L} }[/math]
2) Surface charge density refers to the total amount of charge per unit area. It is modeled by the following equation:
[math]\displaystyle{ \sigma = \frac{Q}{A} }[/math]
3) Volumetric charge density refers to the total amount of charge per unit volume. It is modeled by the following equation:
[math]\displaystyle{ \rho = \frac{Q}{V} }[/math]
A Computational Model
Examples
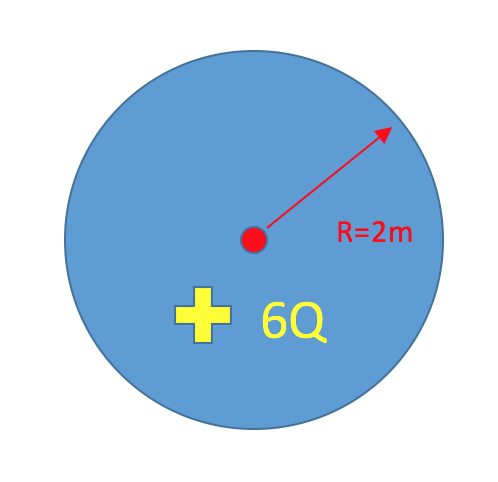
Simple
For the below rod, what is the linear surface charge density?
[math]\displaystyle{ \sigma = \frac{Q}{A} = \frac{+6Q}{pi*(2m)^{2}} = 0.234 \frac{Q}{m^{2}} }[/math]
Middling
Show that both the linear charge density and volume charge density result in the same charge for the infinitesimal portion of a charged rod.
1) The charge density for an infinitesimal portion of the rod can be modeled as the linear charge density times the width of this portion:
Linear charge density for the rod: [math]\displaystyle{ \lambda = \frac{Q}{L} }[/math]
Width of infinitesimal portion: [math]\displaystyle{ dz }[/math]
Charge density of infinitesimal portion: [math]\displaystyle{ dq = \lambda \cdot dz = \frac{Q}{L} \cdot dz }[/math]
2) The charge density for an infinitesimal portion of the rod can be modeled as the volume charge density times the infinitesimal volume of this rod.
Volume charge density for the rod: [math]\displaystyle{ \rho = \frac{Q}{pi*R^{2}} }[/math]
Volume of infinitesimal portion: [math]\displaystyle{ pi*R^{2} \cdot dz }[/math]
Difficult
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
References
This section contains the the references you used while writing this page