Coefficient of Restitution

Claimed by Maria Moreno

The coefficient of restitution measures the amount of Kinetic Energy remains and how much energy is lost after a collision. It also shows the degree of elasticity of a collision. It is defined as the ratio of the difference in initial velocities divided by the difference in final velocities. The coefficient of restitution of a collision is usually between 0 and 1 except in rare cases when energy is released by a collision.

The Main Idea

The coefficient of restitution is a ratio that describes the degree of elasticity of a collision. It is used to solve problems dealing with collisions that are not perfectly elastic or inelastic. The equation that describes the coefficient of restitution involved dividing the difference in the final velocities by the difference in the initial velocity.

Consider objects A and B with initial velocities v_Ai and v_Bi and final velocities v_Af and v_Bf. The coefficient of restitution, e is determined with the following formula:

[math]\displaystyle{ e = \frac{v_{Bf}-v_{Af}}{v_{Ai}-v_{Bi}} }[/math]

The coefficient is a unitless form of measurement as it is the ratio of two velocities and the units cancel.

A Mathematical Model

Consider a perfectly elastic collision between objects A and B where v_Ai and v_Bi refer to the initial velocities of A and B and v_Af and v_Bf refer to the final velocities of A and B.

Start with the conservation of momentum principle which states that
[math]\displaystyle{ \vec{p_i} = \vec{p_f} }[/math]
and
[math]\displaystyle{ m_A\vec{v_{Ai}}+m_A\vec{v_{Bi}}=m_A\vec{v_{Af}}+m_A\vec{v_{Bf}} }[/math] (1)

Remember that for a perfectly elastic collision kinetic energy is also conserved meaning:
[math]\displaystyle{ KE_i = KE_f }[/math]
and
[math]\displaystyle{ \frac{1}{2}m_A v^2_{Ai}+\frac{1}{2}m_A v^2_Bi=\frac{1}{2}m_A v^2_{Af}+\frac{1}{2}m_A v^2_{Bf} }[/math] (2)

Dividing (2) by (1) yields:

[math]\displaystyle{ \vec{v_{Ai}}+\vec{v_{Bi}}=\vec{v_{Af}}+\vec{v_{Bf}} }[/math]
[math]\displaystyle{ 1=\frac{v_{Ai}+v_{Bi}}{v_{Af}+v_{Bf}} }[/math]

[math]\displaystyle{ e=\frac{v_{Ai}+v_{Bi}}{v_{Af}+v_{Bf}} }[/math]

For perfectly elastic collision e=1.

Inelastic Collisions

An inelastic collision is a type of collision where Kinetic Energy is not conserved. In this case the difference in initial velocities will not equal the difference in final velocities. This means that the coefficient of restitution will not equal 1.

Consider the same collision as previously described, except this collision is inelastic and Kinetic Energy is not conserved. Since some of the kinetic energy is dissipated:
[math]\displaystyle{ \frac{1}{2}m_A v^2_{Ai}+\frac{1}{2}m_A v^2_Bi\lt \frac{1}{2}m_A v^2_{Af}+\frac{1}{2}m_A v^2_{Bf} }[/math]

[math]\displaystyle{ \frac{v_{Ai}+v_{Bi}}{v_{Af}+v_{Bf}}\lt 1 }[/math]

[math]\displaystyle{ e=\frac{v_{Ai}+v_{Bi}}{v_{Af}+v_{Bf}}\lt 1 }[/math]

A perfectly inelastic collision (for example when two objects collide and then stick together) has a coefficient of restitution of 0.

Examples

Simple

A ball is traveling at [math]\displaystyle{ 4 \frac{m}{s} }[/math] and collides with a ball. After the collision the ball travels at [math]\displaystyle{ 2.4\frac{m}{s} }[/math] in the opposite direction. Find the coefficient of restitution of the collision.
Start with the definition of the coefficient of restitution:

[math]\displaystyle{ e=\frac{v_{wall_f}-v_{ball_f}}{v_{ball_i}-v_{wall_i}} }[/math]

Then plug in values and solve:

[math]\displaystyle{ e=\frac{0-v_{ball_f}}{v_{ball_i}-0} }[/math]

[math]\displaystyle{ e=\frac{-(-2.4)}{4} }[/math]

[math]\displaystyle{ e=.6 }[/math]

Middling

A hockey puck travels at a constant velocity [math]\displaystyle{ 5\frac{m}{s} }[/math] and is hit by another puck with a velocity of [math]\displaystyle{ 8\frac{m}{s} }[/math]. After the collision, it travels in the opposite direction at 4m/s. This collision has a coefficient of restitution of .55. Find the velocity of the second puck after the collision.
Start with the definition of the coefficient of restitution. We are calling the velocity of the first puck [math]\displaystyle{ v_1 }[/math] and the velocity of the second puck [math]\displaystyle{ v_2 }[/math].
[math]\displaystyle{ e=\frac{v_{1f}-v_{2f}}{v_{2i}-v_{1i}} }[/math]

Solve for [math]\displaystyle{ v_{2f} }[/math]

[math]\displaystyle{ v_{2f}=v_{1f}-e(v_{2i}-v_{1i}) }[/math]

Plug in the values stated in the problem.

[math]\displaystyle{ v_{2f}=4-.55(5-8) }[/math] [math]\displaystyle{ v_{2f}=2.35\frac{m}{s} }[/math]

Difficult

Bouncing Ball Example:

Consider a ball dropped from initial height [math]\displaystyle{ h_0 }[/math]. When it bounces it reaches a height [math]\displaystyle{ h_f }[/math]. Find the coefficient of restitution of this collision.

[math]\displaystyle{ e=\frac{v_{floor_f}-v_{ball_f}}{v_{ball_i}-v_{floor_i}} }[/math]

The floor's velocity is always 0.

[math]\displaystyle{ e=\frac{v_{ball_f}}{v_{ball_i}} }[/math]

Recall the law of conservation of energy:

[math]\displaystyle{ \Delta KE = \Delta PE }[/math]

For the ball from h₀ to h=0 [math]\displaystyle{ \frac{1}{2}mv_{ball_i}^2=mgh_0 }[/math]

[math]\displaystyle{ \frac{1}{2}v_{ball_i}^2=gh_0 }[/math]

[math]\displaystyle{ v_{ball_i}=2\sqrt{gh_0} }[/math]

The same concept can be applied to the second bounce.

[math]\displaystyle{ v_{ball_f}=2\sqrt{gh_f} }[/math]

Plugging this in to the coefficient of restitution expression we get:

[math]\displaystyle{ e=\frac{2\sqrt{mgh_f}}{2\sqrt{mgh_0}} }[/math]

[math]\displaystyle{ e=\frac{\sqrt{h_f}}{\sqrt{h_0}} }[/math]

Connectedness

How is this topic connected to something that you are interested in?
This topic has major connections to sports. As a former high school volleyball player, it is very interesting to think about the collisions that occurred in the game and how the coefficient of restitution is related to those collisions.

How is it connected to your major (Mechanical Engineering)?
The coefficient of restitution is a key concept in the study of Dynamics which is the foundation of many aspects of mechanical engineering. It also has to do with applications of mechanical engineering regarding materials.

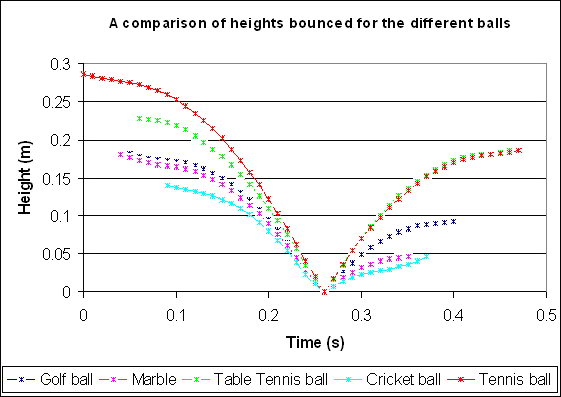
Is there an interesting industrial application? In sports the coefficient of restitution is an important concept especially in sports like golf or tennis where collisions are a frequent and essential part of the game. In these sports sometimes limitations are put on how high the coefficient of restitution can be for certain clubs or bats. The maximum coefficient of restitution allowed in golf for clubs is .82. There have been studies done on the coefficients for different sports balls. These studies usually follow a procedure where different balls are dropped and left to bounce. Then data regarding their initial and final velocities or how high they bounced is recorded. The images below show some of the data from one of these experiments.

See also

Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?

Further reading

Books, Articles or other print media on this topic

References

This section contains the the references you used while writing this page