Wave-Particle Duality

Claimed by vservera3

Wave-particle duality is the concept that states every elementary particle behaves like both a wave and a particle.

The Main Idea

In the 1920s, a French physicist named Louis de Broglie suggested that all matter has wave-like properties. This conclusion was largely the result of two landmark experiments that contradicted each other in almost every way. The first experiment was Thomas Young's double slit experiment, which showed light behaved like a wave. The second experiment was by Albert Einstein, who showed, through his research on the photoelectric effect, that light was made up of discrete packets of energy called photons -- which meant that light also behaved as a particle. This contradiction sent the world of physics as humans knew it into panic.

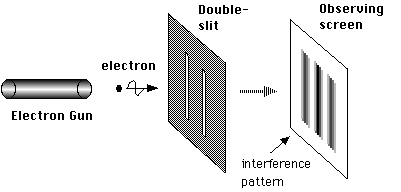
Double slit experiment

The double slit experiment is a deceptively simple experiment that was originally conducted by Thomas Young in the 17th century. In the experiment, Young simply sent a beam of light through two slits and observed the pattern on the surface behind the slits. What he saw was an interference pattern that only could have been present if waves were what went inside two slits. The bright spots occur where the amplitudes of the two waves match (both waves are at their peaks) and the dark spots occur when one wave is at its maximum amplitude and the other is at its minimum.

Photoelectric effect

It was known that when light struck a metal, electrons were liberated from the surface. The intuition was that increasing the intensity of light (shining more light) would liberate more electrons. Albert Einstein found something interesting, though. Varying intensity of light had no effect on how many electrons were liberated. Rather, the frequency of the light determined how many electrons, if any, would be freed. Furthermore, the original theory was that the electrons that would be freed was continuous -- even the smallest amount of light would free some electrons. In fact, this was not the case. Einstein found that there was a minimum threshold frequency that must have been present in order to release electrons at all. This implied there was a minimum amount of energy, or quantum involved in the interaction. This pointed to the fact that light in fact behaved as particles (called photons) which were packets of these quantum energies. This directly conflicted with the double slit experiment.

PhET Simulation for Photoelectric effect

A Mathematical Model

Now that we can treat these particles at the quantum level as waves, we can use many different equations from wave mechanics to describe their behavior. One of the most important equations in dealing with wave like properties of these quantum systems and particles is the Schrödinger equation. The Schrödinger equation is the analog of Newton's second law (F = ma) in quantum mechanics, and describes the wave function over time of a system such as a particle moving in a magnetic field. But rather than a simple linear equation, the Schrödinger equation is a linear partial differential equation:

[math]\displaystyle{ i \hbar \frac{\partial}{\partial t}\Psi(\mathbf{r},t) = \hat H \Psi(\mathbf{r},t) }[/math]

is the general, relativistic (works for particles moving up to close to the speed of light) equation, where [math]\displaystyle{ i }[/math] is the square root of negative 1, [math]\displaystyle{ ħ }[/math] is the Planck constant divided by [math]\displaystyle{ 2pi }[/math], the symbol ∂/∂t indicates a partial derivative with respect to time, Ψ is the wave function of the quantum system, and [math]\displaystyle{ Ĥ }[/math] is the Hamiltonian operator, which represents the total energy of the wave function at different times.

Using the Schrödinger equation involves using the proper form of the Hamiltonian operator that accounts for the kinetic and potential energy of the particles, and using that operator to then solve the partial differential equation. The output wave function contains information about the system at different times.

Examples

The mathematics in solving the Schrodinger equation is quite complicated, but using other simple wave formulas is not very difficult. Two very straightforward formulas involving Planck's constant h, which has a value of [math]\displaystyle{ 6.62607004*10^-34 m^2 }[/math] m^2 kg / s, can be used to relate fundamental properties such as energy E, frequency [math]\displaystyle{ \nu }[/math], and wavelength [math]\displaystyle{ \lambda }[/math].

[math]\displaystyle{ E = h \nu }[/math] (1)

[math]\displaystyle{ \lambda = \frac{h}{p} . }[/math] (2)

Another very useful equation is that the frequency and the wavelength of a particle are inversely proportional, and multiply to the speed of light, c.

[math]\displaystyle{ c = \lambda\nu }[/math] (3)

Ex. 1

Microwave ovens emit microwave energy with a wavelength of 12.9 cm. What is the energy of exactly one photon of this microwave radiation?

Here we need to use equations 1 and 3.

Next we define our constants.

[math]\displaystyle{ c= 2.998*10^8 m/s }[/math] (this problem wants us to use this number for speed of light), [math]\displaystyle{ h=6.626*10^34J-s }[/math]

Now we simply plug in, making sure that our units match (convert 12.9cm to meters = 0.129m)

[math]\displaystyle{ 2.998*10^8 m/s = .129 * v }[/math]

[math]\displaystyle{ v = 2,324,031,008 Hz }[/math]

Now that we found v, we can solve for E.

[math]\displaystyle{ E = 2,324,031,008 Hz * 6.626*10^-34 }[/math]

[math]\displaystyle{ E= 1.53990294*10^-24 }[/math]

[math]\displaystyle{ E= 1.54*10^-24 }[/math]

Ex. 2

A radio station broadcasts at a frequency of 590 KHz. What is the wavelength of the radio waves?

We need to use equation 3.

First we convert KHz to Hz.

[math]\displaystyle{ 590 }[/math] KHz = [math]\displaystyle{ 590*10^3 }[/math] Hz

[math]\displaystyle{ (3*10^8)/(590*10^3) }[/math] = [math]\displaystyle{ 500 }[/math]m = [math]\displaystyle{ \lambda }[/math]

[math]\displaystyle{ \lambda }[/math] = 500m.

Connectedness

1.How is this topic connected to something that you are interested in?

For a while I had been interested in the strange nature of quantum mechanics. The pure fact that particles could act as waves was simply alluring. In the future it would be great if, even as a biology major, work in a field that had some aspect of quantum research associated.

2.How is it connected to your major?

Extensive, high level research in biology, my major, has shown that during photosynthesis, plants benefit from the quantum properties of the light coming from the sun, and are able to use it to transport energy more efficiently. This groundbreaking discovery could be the key to discovering extremely effective cures for diseases that currently are uncurable or are very costly to treat.

3.Is there an interesting industrial application?

Right now, since quantum computing is not effective or cheap enough for companies to use, industry use is limitied. But common lab use is in electron microscopy - it is possible by exploiting the high frequencies of electrons, meaning that one can see objects much smaller than those that can only be seen with visible light.

History

Throughout the 1800s, scientists one by one, such as John Dalton and Ernest Rutherford theorized and discovered elementary particles. Those discoveries in and of themselves were groundbreaking, but of course, scientists pursued these further. It was then that a contradiction arose in two experiments, as mentioned in the above sections, and things went haywire. Newton's classical mechanics had no way of explaining phenomenon like this, so a new field of quantum mechanics was born to study physics of particles on minute scales. The 1900s included scientists like Richard Feynman and Erwin_Schr%C3%B6dinger (the scientist the above differential equation was named after) that made leaps in QM. Currently, scientists are working on applying quantum effects to computing.

See also

This topic is a big idea in the field of quantum mechanics, but there are many other interesting concepts to further explore:

-Quantum entanglement

-Theory of everything

-Standard Model

References

This section contains the the references you used while writing this page:

All pictures were from Wikimedia Commons, and references are already hyperlinked to key words in the text.