Elastic Collisions: Difference between revisions
| Line 10: | Line 10: | ||
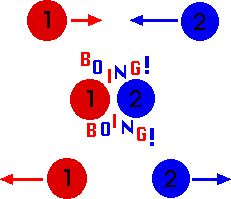
And I love playing pool because every time a ball hits another and they bounce off one another I’m witnessing an elastic collision so basically I’m a physicist in the lab. The image below demonstrates the main idea of an elastic collision. Boing!! | And I love playing pool because every time a ball hits another and they bounce off one another I’m witnessing an elastic collision so basically I’m a physicist in the lab. The image below demonstrates the main idea of an elastic collision. Boing!! | ||
It's important to note that with macroscopic systems there are no perfectly elastic collisions because there's always at least a dab of dissipation (like some thermal energy given off), but most are nearly elastic. The only time there are perfect collisions is on a microscopic level when atomic systems with quantized energy collide, but that's only if there is enough energy available to raise the systems to an excited quantum state but quantum energy is really a whole other topic. Let's focus on elastic collisions! | It's important to note that with macroscopic systems there are no perfectly elastic collisions because there's always at least a dab of dissipation (like some thermal energy given off), but most are nearly elastic. The only time there are perfect collisions is on a microscopic level when atomic systems with quantized energy collide, but that's only if there is enough energy available to raise the systems to an excited quantum state-- but quantum energy is really a whole other topic. Let's focus on elastic collisions! | ||
[[File: boing.gif]] | [[File: boing.gif]] | ||
Revision as of 23:20, 5 December 2015
CLAIMED BY KINGRAM7
The Main Idea
So what exactly is an elastic collision? I know you’re thinking, “Oh I know all about elasticity,” but LOL this is not bubble gum or rubber bands guys!
An elastic collision is a collision between two or more objects in which there is no loss in kinetic energy before and after the collision. If we assume that the colliding objects are part of the system and that there is no force from the surroundings, the final kinetic energy is still in the same form as it was initially. To keep it simple, this means that kinetic energy in= kinetic energy out. Remember how your parents always told you what goes in must come out? They were talking about elastic collisions... probably.
Additionally, elastic collisions are a wonderful representation of the conservation of momentum which states that the momentum of an isolated system is constant. For an isolated system undergoing an elastic collision momentum in = momentum out.
And I love playing pool because every time a ball hits another and they bounce off one another I’m witnessing an elastic collision so basically I’m a physicist in the lab. The image below demonstrates the main idea of an elastic collision. Boing!!
It's important to note that with macroscopic systems there are no perfectly elastic collisions because there's always at least a dab of dissipation (like some thermal energy given off), but most are nearly elastic. The only time there are perfect collisions is on a microscopic level when atomic systems with quantized energy collide, but that's only if there is enough energy available to raise the systems to an excited quantum state-- but quantum energy is really a whole other topic. Let's focus on elastic collisions!
A Mathematical Model
Let’s take what we know about elastic collisions and translate them into that weird language called math. We know that there is no loss in kinetic energy before and after an elastic collision. So,

(Initial kinetic energy = final kinetic energy)
This simple principal can be expanded into:
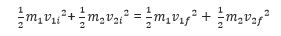
Starting from the left side we have m1 and m2 which are the masses of object 1 and 2 respectively, and v1i and v2i represent their initial velocities respectively. On the right side of the equation, the final kinetic energy, it’s the same equation just different numbers! For the final kinetic energy, unless stuff is breaking or its otherwise stated in the problem, you can assume the masses won’t change BUT the velocities may. Imagine if you toss a pool ball towards another one that is initially at rest. The one that is at rest will move after it is hit, so there is a change in velocity! However, please remember that there is no overall change in kinetic energy. Let’s say the mass of our pool balls are 2 kilograms and I will make up some speeds. Applying the formula from above we get:
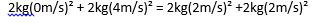
As you see the final velocities changed. One ball was initially at rest but it wasn't after the collision because it was struck by a ball that was already moving...But there was no change in kinetic energy because 32=32 yay! Put it in your calculator and see for yourself.
A Computational Model
The link below demonstrates a basic car crash elastic collision using MATLAB. Take note of the changes in displacement and the time.
Elastic Collision MATLAB model
Examples
Be sure to show all steps in your solution and include diagrams whenever possible
Simple
Okay let’s start with a simple example like the ones you don't see on the test.
Jay and Sarah are best friends. Since they’re best friends they both weigh 55 kg. Jay hadn’t seen Sarah in a long time so when she saw her she ran to her with a velocity of <4,0,0> m/s. Instead of a hug, they were both too excited and collided and bounced back off of each other, and Sarah flew back with a velocity of <7,0,0> m/s. What was Jay’s final velocity?
Okay, so first let’s think about what we know. This is an elastic collision, so as we mentioned before: Pf = Pi. Breaking that down, we have:
m1v1 + m2v2 = m1v1f + m2v2f, and we are looking for v1f. So let’s rearrange the equation:
v1f= (m1v1 + m2v2) – (m2v2f) / m1
Now, let’s plug in the numbers!
V1f= (55*<4,0,0> + 55*<0,0,0>) – (55*<7,0,0>)/(55)
V1f= <-3,0,0> m/s (Don't forget it's negative because Jay is going in the opposite direction that she started out,not because she's incredibly slow.)
Middling
Difficult
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
Internet resources on this topic
References
This section contains the the references you used while writing this page