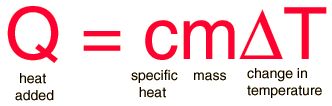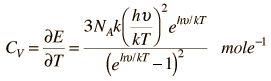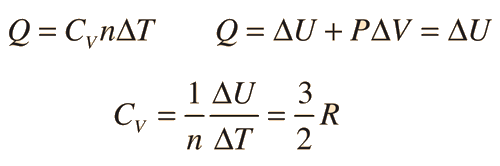|
|
| Line 1: |
Line 1: |
| PLEASE DO NOT EDIT THIS PAGE. COPY THIS TEMPLATE AND PASTE IT INTO A NEW PAGE FOR YOUR TOPIC.
| | |
|
| |
|
| Short Description of Topic | | Short Description of Topic |
| Line 96: |
Line 96: |
|
| |
|
|
| |
|
| ===A Mathematical Model=== | | ===Specific Heats of Gases=== |
|
| |
|
| What are the mathematical equations that allow us to model this topic. For example <math>{\frac{d\vec{p}}{dt}}_{system} = \vec{F}_{net}</math> where '''p''' is the momentum of the system and '''F''' is the net force from the surroundings.
| | Specific heats of gases are generally expressed in their molar form due to the undefined volume or pressure of a gas. Usually only one is held constant. |
|
| |
|
| ===A Computational Model===
| |
|
| |
|
| How do we visualize or predict using this topic. Consider embedding some vpython code here [https://trinket.io/glowscript/31d0f9ad9e Teach hands-on with GlowScript]
| | There are two specific heats for gases., one for gases at a constant volume and one gases at a constant pressure. For a constant volume process with a monoatomic ideal gas the first law of thermodynamics gives |
|
| |
|
| ==Examples==
| | [[File:Specific Heat of Gas.gif]] |
|
| |
|
| Be sure to show all steps in your solution and include diagrams whenever possible
| |
|
| |
|
| ===Simple=== | | ===Simple=== |
| Line 152: |
Line 150: |
|
| |
|
|
| |
|
| A Computational Model[edit]
| |
|
| |
| How do we visualize or predict using this topic. Consider embedding some vpython code here Teach hands-on with GlowScript
| |
|
| |
| First Law[edit]
| |
|
| |
| The first law of thermodynamics defines the internal energy (E) as equal to the difference between heat transfer (Q) into a system and work (W) done by the system. Heat removed from a system would be given a negative sign and heat applied to the system would be given a positive sign. Internal energy can be converted into other types of energy because it acts like potential energy. Heat and work, however, cannot be stored or conserved independently because they depend on the process. This allows for many different possible states of a system to exist. There can be a process known as the adiabatic process in which there is no heat transfer. This occurs when a system is full insulated from the outside environment. The implementation of this law also brings about another useful state variable, enthalpy.
| |
|
| |
| A Mathematical Model[edit]
| |
|
| |
| E2 - E1 = Q - W
| |
|
| |
| Second Law[edit]
| |
|
| |
| The second law states that there is another useful variable of heat, entropy (S). Entropy can be described as the disorder or chaos of a system, but in physics, we will just refer to it as another variable like enthalpy or temperature. For any given physical process, the combined entropy of a system and the environment remains a constant if the process can be reversed. The second law also states that if the physical process is irreversible, the combined entropy of the system and the environment must increase. Therefore, the final entropy must be greater than the initial entropy.
| |
|
| |
| Mathematical Models[edit]
| |
|
| |
| delta S = delta Q/T Sf = Si (reversible process) Sf > Si (irreversible process)
| |
|
| |
| Examples[edit]
| |
|
| |
| Reversible process: Ideally forcing a flow through a constricted pipe, where there are no boundary layers. As the flow moves through the constriction, the pressure, volume and temperature change, but they return to their normal values once they hit the downstream. This return to the variables' original values allows there to be no change in entropy. It is often known as an isentropic process.
| |
|
| |
| Irreversible process: When a hot object and cold object are put in contact with each other, eventually the heat from the hot object will transfer to the cold object and the two will reach the same temperature and stay constant at that temperature, reaching equilibrium. However, once those objects are separated, they will remain at that equilibrium temperature until something else acts upon it. The objects do not go back to their original temperatures so there is a change in entropy.
| |
|
| |
| Connectedness[edit]
| |
| 1.How is this topic connected to something that you are interested in?
| |
| 2.How is it connected to your major?
| |
| 3.Is there an interesting industrial application?
| |
|
| |
| History[edit]
| |
|
| |
| Thermodynamics was brought up as a science in the 18th and 19th centuries. However, it was first brought up by Galilei, who introduced the concept of temperature and invented the first thermometer. G. Black first introduced the word 'thermodynamics'. Later, G. Wilke introduced another unit of measurement known as the calorie that measures heat. The idea of thermodynamics was brought up by Nicolas Leonard Sadi Carnot. He is often known as "the father of thermodynamics". It all began with the development of the steam engine during the Industrial Revolution. He devised an ideal cycle of operation. During his observations and experimentations, he had the incorrect notion that heat is conserved, however he was able to lay down theorems that led to the development of thermodynamics. In the 20th century, the science of thermodynamics became a conventional term and a basic division of physics. Thermodynamics dealt with the study of general properties of physical systems under equilibrium and the conditions necessary to obtain equilibrium.
| |
|
| |
| See also[edit]
| |
|
| |
| Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
| |
|
| |
| Further reading[edit]
| |
|
| |
| Books, Articles or other print media on this topic
| |
|
| |
| External links[edit]
| |
|
| |
| Internet resources on this topic
| |
|
| |
| References[edit]
| |
|
| |
| https://www.grc.nasa.gov/www/k-12/airplane/thermo0.html http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/thereq.html https://www.grc.nasa.gov/www/k-12/airplane/thermo2.html http://www.phys.nthu.edu.tw/~thschang/notes/GP21.pdf http://www.eoearth.org/view/article/153532/
| |
|
| |
|
| |
| Category: Which Category did you place this in?
| |
|
| |
|
| |
|
| |
| Navigation menu
| |
|
| |
|
| |
| Fjoseph96
| |
| Talk
| |
| Preferences
| |
| Watchlist
| |
| Contributions
| |
| Log out
| |
|
| |
|
| |
| Page
| |
|
| |
|
| |
| Discussion
| |
|
| |
|
| |
|
| |
|
| |
| Read
| |
|
| |
|
| |
| Edit
| |
|
| |
|
| |
| View history
| |
|
| |
|
| |
| Watch
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
|
| |
|
Revision as of 22:23, 5 December 2015
Short Description of Topic
The Main Idea
The most common definition is that specific heat is the amount of heat needed to raise the temperature of a mass by 1 degree. The relationship between heat and temperature change is best defined by constant "C" in the equation
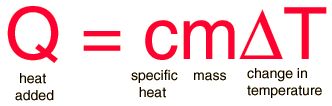
The relationship does not apply if a phase change is occurs because the heat added or removed during a phase change does not necessarily change the temperature. The specific heat most commonly known specific heat is 4.16 J/g degrees Celsius, which is the specific heat for water. The specific heat per gram for water is much higher than that for a metal. Therefore, there are two separate ways to calculate specific heats. Traditionally, it is more acceptable to compare specific heats on a molecular level.
The molar specific heats of most solids at room temperature are almost the same, which agrees with the Law of Dulong and Petit. At lower temperatures the specific heats drop as atomic processes become more relevant. The lower temperature behavior is explained by the Einstein-Debye model of specific heat.
Law of Dulong and Petit
[edit]
The specific heat of copper is 0.386 Joules/gram degrees Celsius while the specific heat of Aluminum is 0.900 Joules/gram Celsius. Why is there such a difference? Specific heat is measured in Energy per unit mass, but it should be measured in Energy per mole for more similar specific heats for solids. The similar molar specific heats for solid metals are what define the Law of Dulong and Petit.

The specific heats of metals, therefore should all be around 24.94 J/mol degrees Celsius. The specific heat at constant volume should be just the temperature derivative of that energy.
Copper 0.386 J/gm K x 63.6 gm/mol = 24.6 J/mol K
Aluminum 0.900 J/gm K x 26.98 gm/ mol = 24.3 J/mol K
Einstein Debye Model
[edit]
For low temperatures, Einstein and Debye found that the Law of Dulong and Petit was not applicable. At lower temperatures, it was found that atomic interactions were deemed significant in calculating the molar specific heat of an object.
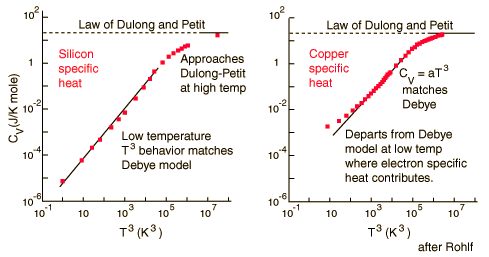
According to the Einstein Debye Model for Copper and Aluminum, two solid metals, specific heat varies much at lower temperatures and goes much below the Dulong-Petit Model. This is due to increased effects on specific heat by interatomic forces. However, for very high temperature values, the Einstein-Debye Model cannot be used. In fact, at high temperatures, Einstein's expression of specific heat, reduces to the Dulong-Petit mathematical expression.
Here is the Einstein Debye Equation:
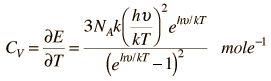
For high Temperatures it may be reduced like this:

This actually reduces to the Dulong-Petit Formula for Specific Heat:

Specific Heats of Gases
Specific heats of gases are generally expressed in their molar form due to the undefined volume or pressure of a gas. Usually only one is held constant.
There are two specific heats for gases., one for gases at a constant volume and one gases at a constant pressure. For a constant volume process with a monoatomic ideal gas the first law of thermodynamics gives
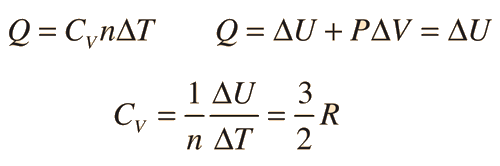
Simple
Middling
Difficult
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Are there related topics or categories in this wiki resource for the curious reader to explore? How does this topic fit into that context?
Further reading
Books, Articles or other print media on this topic
External links
[1]
References
This section contains the the references you used while writing this page
Template
Claimed by Felix Joseph
Main page
Recent changes
Random page
Help
Tools
What links here
Related changes
Upload file
Special pages
Printable version
Permanent link
Page information
This page was last modified on 29 November 2015, at 23:04.
This page has been accessed 525 times.
Privacy policy
About Physics Book
Disclaimers