Rayleigh Effect: Difference between revisions
Ashankar35 (talk | contribs) |
Ashankar35 (talk | contribs) |
||
| Line 19: | Line 19: | ||
''λ'' = wavelength of the light | ''λ'' = wavelength of the light | ||
''θ'' = the scattering angle | ''θ'' = the scattering angle | ||
Therefore, the intensity of the scattered light is inversely proportional to the fourth power of the wavelength of the incident light. | |||
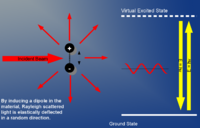
[[File:Rayleigh_Effect.png|200px|thumb|Rayleigh Effect at atomic level]] | |||
==Examples== | ==Examples== | ||
Revision as of 23:44, 5 December 2015
Rayleigh scattering, named after the British physicist Lord Rayleigh (John William Strutt),is the (dominantly) elastic scattering of light or other electromagnetic radiation by particles much smaller than the wavelength of the radiation.
The Main Idea
When light strikes small particles, it bounces off in a different direction in a process called scattering. Rayleigh scattering is the scattering that occurs when the particles are smaller than the wavelength of the light. This is the dispersion of electromagnetic radiation by particles that have a radius less than approximately 1/10 the wavelength of the radiation. The particles may be individual atoms or molecules. It can occur when light travels through transparent solids and liquids, but is most prominently seen in gases. Rayleigh scattering results from the electric polarizability of the particles. The oscillating electric field of a light wave acts on the charges within a particle, causing them to move at the same frequency. The particle therefore becomes a small radiating dipole whose radiation we see as scattered light.
A Mathematical Model
Lord Rayleigh calculated the scattered intensity from dipole scatterers much smaller than the wavelength to be:
- [math]\displaystyle{ I = I_0 \frac{8\pi^4\alpha^2}{\lambda^4 R^2}(1+\cos^2\theta). }[/math]
I = resulting intensity of scattered light
I0 = intensity of incident light
α = molecular polarizability
λ = wavelength of the light
θ = the scattering angle
Therefore, the intensity of the scattered light is inversely proportional to the fourth power of the wavelength of the incident light.
Examples
The sun's light is a mix of violet, blues, greens through to reds. Blues and violets have the shortest wavelengths, that of blue is ~450 nanometres. Air molecules, mostly nitrogen and oxygen, are 1000X smaller still. They interact only very weakly with visible light but with their enormous numbers in the atmosphere the Rayleigh effect is clearly seen. Air molecules individually scatter sunlight it into all directions. Blue light is scattered much more strongly than longer wavelengths. The air above looks blue from that scattered sunlight. All other colors are scattered as well but progressively more weakly towards red. This is because the intensity of scattered light is inversely proportional to the fourth power of the wavelength of incident light and blue having the shortest wavelenth is scattered more, making the sky appear blue. The sky is not pure blue as it also contains a small proportion of other scattered colours.
Connectedness
Rayleigh effect gives an interesting interaction between light and particles smaller than the wavelength of light. This explores an interesting relationship between the particle and wave nature of light. It is used in the development and characterization of systems employing laser-induced Rayleigh light scattering with digital data acquisition as a concentration probe in the turbulent flow field of a binary gas mixture. It also used to analyze the composition of organic solutions . In addiction it is used a lot in laser-based nonintrusive techniques that have been developed for combustion diagnostics. Laser Rayleigh scattering (LRS) has received increased attention in studying turbulent combustion due to its many valuable characteristics
History
Rayleigh used “dimensional analysis” in his work. Rayleigh published a paper in which he used dimensional analysis to show that the intensity of light in the sky, if scattered from particles much smaller than the wavelength of incident light, should vary as λ-4. Therefore, blue light should be scattered 16× more than red light; this explained the blue sky.
In Rayleigh’s paper, “On the Light from the Sky, Its Polarization and Colour,” he obtained the inverse fourth power dependence of the ratio of the scattered-to-incident illumination on wavelength by balancing the exponents on both sides of a scattering equation.
Rayleigh returned to this scattering problem several times and, in 1899, he derived the expression for the incident wavelength, the intensity and degree of polarization of the scattered light as a function of wavelength, angle and refractive index of the scattering particles. In his second paper on light scattering, which was published in 1871, Rayleigh posited that the molecules comprising the air are the scattering objects in the sky.
See also
http://www.physicsbook.gatech.edu/Light_Scaterring:_Why_is_the_Sky_Blue
Further reading
http://journals.cambridge.org/action/displayAbstract?fromPage=online&aid=377076
External links
References
http://science.jrank.org/pages/5752/Rayleigh-Scattering.html
