The Differential Form of Ampere's Law

Many physical laws taught in Physics I and II are only correct at non-relativistic speeds (where the speed is much less than the speed of light). This is caused by relativistic retardation, a term for how changes in magnetic and electric fields propagate at the speed of light so they cannot be measured instantly. Typically this is not an issue if the particles are moving much slower than the speed of light because although these physical laws are technically incorrect, the margin of error is so small that it is irrelevant. As particles approach speeds close to the speed of light these differences can become significant and methods for finding electric or magnetic fields (such as the Biot-Savart law) are no longer accurate. This is not true for Ampere's Law which makes it useful for problems involving particles moving at near light speeds.

Curl

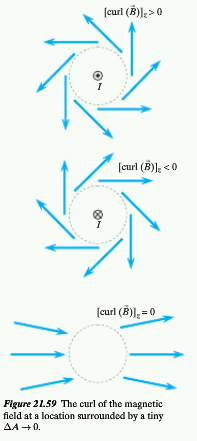
To have a model that is consistent with the theory of relativity, the property of a magnetic field called the "curl" must be utilized. The curl is the path integral of magnetic field per unit area, in the limit as the area goes to zero. This is useful because its value is proportional to the current density at the same location and time so there is an established relationship. This is known as a local relationship because both are evaluated at the same place and time, making it relativisticly correct because it isn't effected by relativistic retardation.

Lecture Video: https://www.youtube.com/watch?v=mj2ahFjnpmY

A Mathematical Model

Curl is the measurement of how much magnetic field loops around a line. It is a vector in the same direction of the flow of current.

Definition of curl:

Curl can also be expressed in terms of a "del" operator or gradient operator. This is the same operator that relates the (x, y, z) components of electric field to voltage. Expressing the components as the the partial derivative of voltage is the gradient of it.

Gradient Operator:

A Computational Model

The direction of curl is given by the right hand rule by putting your thumb in the direction of the current. The way your hand curls is the way the magnetic field curls.

Examples

Connectedness

1. The differential form of Ampere's Law interests me because it is one of the first laws that we learned that is relativistically correct, although it is not the complete form of Ampere's Law.
2. As a ME major I imagine Ampere's Law will pop up again in either fluids or thermodynamics.
3. An interesting application of Ampere's Law is in MRI machines to be able to find the magnetic field around a loop.

See also

1. Gauss's Law
2. The Integral form of Ampere's Law
3. Gradient Operations

Further reading

http://www.physnet.org/modules/pdf_modules/m138.pdf

http://ww3.haverford.edu/physics-astro/songs/ampere.PDF

References

http://www.physics.byu.edu/faculty/rees/220/book/Lesson8.pdf Matter and Interactions, 4th Edition