Charged Ring

This article will describe the Electric Field created by a uniformly charged thin ring and how to calculate the value of this field.

The Main Idea

Objects that create electric fields come in various shapes, including circular rings. Rings can be thought of as just a collection of Point Charges organized into a circular ring shape. This makes analyzing the ring mathematically much easier to do.

A Mathematical Model

The following example of the calculation of the electric field produced by a uniformly charged ring is based on the equation for the electric field of a Point Charge. It also takes advantage of the principles of integration.

A Computational Model

This VPython code is a representation of adding up the electric fields created by individual pieces of a ring to figure out its electric field.

Step-by-Step Example

Below is an example of calculating the value and direction of the Electric Field caused by a ring positioned in the xy-plane with a radius [math]\displaystyle{ R }[/math] and total charge [math]\displaystyle{ q }[/math]. Physics 2212 only requires mastery of the simplest case -- the field at a location along the line that goes through the center of the ring, perpendicular to the plane that the circle is in. We'll call that line the [math]\displaystyle{ z-axis }[/math].

(1) Cut Up the Charge

Pick an arbitrary piece of the ring to act as a Point Charge and assign it an angular length Δθ. Draw the Electric Field created by this point charge.

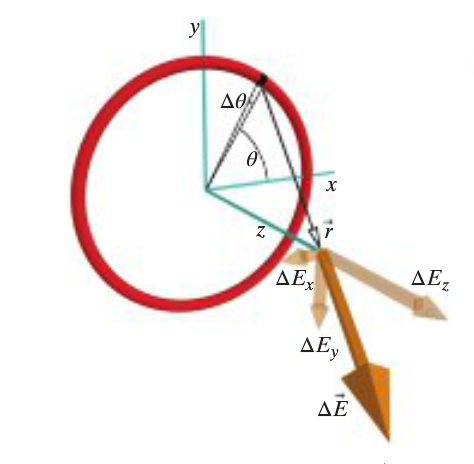
(2) Write E for One Piece

Assume that [math]\displaystyle{ θ = 0 }[/math] is along the [math]\displaystyle{ x-axis }[/math]. We know that our integration variable is θ because we are adding up the pieces around the circle.

[math]\displaystyle{ x-axis }[/math] [math]\displaystyle{ \ r =\{\lt obs.loc\gt } - {\lt source\gt } = {\lt 0,0,z\gt } - {\lt Rcosθ, Rsinθ, 0\gt } }[/math] [math]\displaystyle{ \ E=\frac{Q/A}{\epsilon_0 } }[/math] [math]\displaystyle{ \ E=\frac{Q/A}{\epsilon_0 } }[/math] [math]\displaystyle{ \ E=\frac{Q/A}{\epsilon_0 } }[/math] [math]\displaystyle{ \ E=\frac{Q/A}{\epsilon_0 } }[/math]

The x and y components of the electric field cancel, so the only remaining field is in the z-direction.

Connectedness

Calculating the electric field of a charged ring may seem like another exercise to practice visualizing the way a collection of charge can create a field and influence other objects around it, but it becomes very important in the study of Category:Simple Circuits.

Electric fields created by rings of charge are the source of currents in circuits, which makes these little charged rings one of the most important components of daily life for almost all Americans and 83% of the citizens of the world. Rings of charge compounded into hollow wires of charge are a central part of past, present, and future human innovation.

History

In 1831, Michael Faraday showed that when a wire moves within the field of a magnet, it causes an electric current to flow along the wire. Then James Maxwell published his work, Dynamical Theory of the Electric Field, establishing the connections between electricity and magnetism.

See also

The section on Category:Fields will give some insight into how rings behave in comparison to distributions of charge that form other shapes, and the section entitled Category:Simple Circuits will show you how this charged ring calculation can be used in circuits and real-world applications.

External Links/References

"Electric Field on the Axis of a Ring of Charge". University of Delaware Physics Library. Adapted from Stephen Kevan's lecture on Electric Fields and Charge Distribution. April 8, 1996. http://www.physics.udel.edu/~watson/phys208/exercises/kevan/efield1.html

Chabay, R., & Sherwood, B. (2015). Matter and Interactions (4th ed., Vol. 2, pp. 597-599). Wiley.

Energy Access Database. (n.d.). Retrieved December 6, 2015, from http://www.worldenergyoutlook.org/resources/energydevelopment/energyaccessdatabase/

Nielsen, G. (n.d.). James Clerk Maxwell. Retrieved December 6, 2015, from https://geoffneilsen.wordpress.com/tag/electric-field/

Work in progress! - afrancis38