Resolving Power: Difference between revisions
Estaniforth (talk | contribs) No edit summary |
Estaniforth (talk | contribs) No edit summary |
||
| Line 27: | Line 27: | ||
When the two stars have very little angular separation, although the theory may suggest that an increased aperture or magnification would suffice in resolving the two images, diffraction proves this untrue. Each star cannot be considered a point of light but instead a disk of light. If there is too much overlap then increased aperture or magnification simply amplifies the blur of light. | When the two stars have very little angular separation, although the theory may suggest that an increased aperture or magnification would suffice in resolving the two images, diffraction proves this untrue. Each star cannot be considered a point of light but instead a disk of light. If there is too much overlap then increased aperture or magnification simply amplifies the blur of light. | ||
However, in the case that the stars' Airy disks touch, | However, in the case that the stars' Airy disks touch, the two stars are at Dawes limit. In this situation it is possible to differentiate them and determine the minimum angle with, ''0.12/''<math>a</math>''arc seconds''. (<math>a</math> - diameter of the aperture in meters) | ||
[[File:Airydisk.gif]] | If the center of the Airy disk of one star falls on the first dark ring of other star's diffraction pattern. These too can be distinguished and the minimum angle is calculated with <math>\frac{13}{a}</math>''arc seconds''. (<math>a</math> - diameter of the aperture in meters) | ||
<center>[[File:Airydisk.gif]]</center> | |||
==Applications== | ==Applications== | ||
Revision as of 20:11, 6 December 2015
Claimed by estaniforth3
The Main Idea
Resolving power is the measure of an optical system's ability to differentiate between the images of objects close together or separate similar wavelengths of radiation and therefore display fine detail. In an ideal situation, this quantity is dependent on two components of the radiation, the aperture (the space through which light passes in an optical system) and wavelength (the distance between crests in a wave). However in real life applications the resolving power is limited by the effects of diffraction, the effect on a wave when it encounters an obstacle.

The Rayleigh Criterion for Minimal Image Resolution
Lord Rayleigh (John William Strutt) determined that, given two point light sources, the center of the image of the first source will fall on the first diffraction ring of the second source. Because of this, there is a minimum angle (in radians) between the two sources (as viewed by the system) for the two sources to be at least marginally resolvable (distinguishable). In ideal circumstances it would be defined as [math]\displaystyle{ \frac{λ}{a} }[/math], however factoring in diffraction:
Angular limit of Resolution [math]\displaystyle{ = \frac{1.22λ}{a} }[/math]
λ - wavelength in meters, [math]\displaystyle{ a }[/math] - diameter of the aperture in meters
The resolving power can be found by calculating the inverse of the angular limit of resolution.
Resolving power [math]\displaystyle{ = \frac{a}{1.22λ} }[/math]
λ - wavelength in meters, [math]\displaystyle{ a }[/math] - diameter of the aperture in meters
Dawes and Rayleigh limits
However once you reach the scale of stars and telescopes, there are three different possible scenarios.
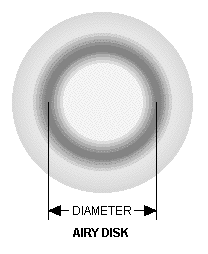
When the two stars have very little angular separation, although the theory may suggest that an increased aperture or magnification would suffice in resolving the two images, diffraction proves this untrue. Each star cannot be considered a point of light but instead a disk of light. If there is too much overlap then increased aperture or magnification simply amplifies the blur of light.
However, in the case that the stars' Airy disks touch, the two stars are at Dawes limit. In this situation it is possible to differentiate them and determine the minimum angle with, 0.12/[math]\displaystyle{ a }[/math]arc seconds. ([math]\displaystyle{ a }[/math] - diameter of the aperture in meters)
If the center of the Airy disk of one star falls on the first dark ring of other star's diffraction pattern. These too can be distinguished and the minimum angle is calculated with [math]\displaystyle{ \frac{13}{a} }[/math]arc seconds. ([math]\displaystyle{ a }[/math] - diameter of the aperture in meters)
Applications
Be sure to show all steps in your solution and include diagrams whenever possible
Telescopes
Microscopes
Connectedness
- How is this topic connected to something that you are interested in?
- How is it connected to your major?
- Is there an interesting industrial application?
History
Put this idea in historical context. Give the reader the Who, What, When, Where, and Why.
See also
Further reading
Pedrotti, Frank L., Leno M. Pedrotti, and Leon S. Pedrotti. Introduction to Optics, 3rd ed. San Francisco: Addison Wesley, 2007.
Serway, Raymond A., Jerry S. Faughn, Chris Vuille, and Charles A. Bennet. College Physics, 7th ed. Belmont, Calif.: Thomson Brooks/Cole, 2006.
Young, Hugh D., and Roger A. Freedman. University Physics, 12th ed. San Francisco: Addison Wesley, 2007.
External links
Internet resources on this topic
References
"Optics." Encyclopedia of Physical Science. Facts On File, 2009. Science Online. Web. 2 Dec. 2015. <http://online.infobase.com/HRC/LearningCenter/Details/8?articleId=299135>.