Biot-Savart Law: Difference between revisions

Revision as of 17:10, 10 April 2016

CLAIMED BY JULIANNE OLIVER SPRING 2016

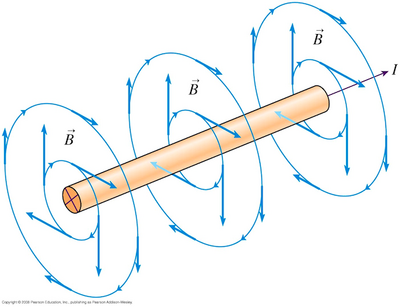
The Biot-Savart (pronounced bee-yo sahv-ar) Law is an equation that describes the quantitative relationship between a moving point charge and the magnetic field it generates. This law is seen as a magnetic equivalent of Coulomb's Law[3], and states that the magnetic field decreases with the square of a distance from a point charge. This law is consistent with Ampere's Law and Gauss's Law for magnetism. It is so named for Jean-Baptiste Biot and Felix Savart who discovered the law in 1820.

The Main Idea

A moving point produces a magnetic field. In addition to the electric fields created by point charges, magnetic fields are another field that a point charge can create. In contrast to an electric field, a point charge must have some velocity in order to create a magnetic field.

A Mathematical Model

The general formula for a single charge is [math]\displaystyle{ \vec B=\frac{\mu_0}{4\pi}\frac{q\vec v\times\hat r}{r^2} }[/math] where [math]\displaystyle{ \mu_0 }[/math] is the constant [math]\displaystyle{ 1e-7 \frac{tesla * m^2}{coloumb * \frac{m}{s}} }[/math] exactly. [math]\displaystyle{ \vec v }[/math] is the velocity of the point charge [math]\displaystyle{ q }[/math], and [math]\displaystyle{ \hat r }[/math] is the unit vector pointing from the source location towards the observation location (remember [math]\displaystyle{ r= r(obs)-r(source) }[/math])

Direction of Magnetic Field The direction of the magnetic field is not as simple as the direction of an electric field. The magnetic field's direction is given by crossing the velocity vector with the [math]\displaystyle{ \hat r }[/math] vector. The product of crossing two vectors is always a vector perpendicular to both of the original vectors! The cross product is at a maximum when the angle between the two vectors equals ninety degrees. The cross product is zero when two vectors are parallel to one another (the angle between the two vectors equals zero or 180).

A Special Note: When dealing with a moving electron, be sure to take into account the negative charge on the electron; this negative charge will switch the sign of the cross product between [math]\displaystyle{ \vec v }[/math] and [math]\displaystyle{ \hat r }[/math].

Magnitude of Magnetic Field The magnitude of the magnetic field is given by [math]\displaystyle{ B=\frac{\mu_0}{4\pi}\frac{qv sin(\theta)}{r^2} }[/math]

A Computational Model

Check out this link: https://trinket.io/glowscript/93785debae for a look at a moving point charge acted on by a magnetic force. This magnetic force acts on the point charge since the point charge is moving with a certain velocity. Magnetic force goes hand-in-hand with magnetic field. Just as a point charge can only create a magnetic field if the point charge is moving, a point charge can only feel the force from a magnetic field if the point charge has a velocity. This computational model shows how a moving point charge, which creates its own magnetic field, is acted on by an external magnetic field.

For a computational model of a wire carrying current, see the wiki page on the Biot-Savart Law for Currents [[4]].

Examples

Example 1

An electron located at the origin is moving at [math]\displaystyle{ 2e8 }[/math] m/s in the +x direction. What is the magnetic field at [math]\displaystyle{ \lt 200, -300, 0\gt }[/math] m due to the moving electron?

Example 2

A proton is located on the +x axis and is moving with a velocity [math]\displaystyle{ \vec v }[/math] in the -y direction. What is the magnitude of the magnetic field at [math]\displaystyle{ \lt 0, 0, z\gt }[/math] at [math]\displaystyle{ \theta = 34 }[/math] degrees from [math]\displaystyle{ \vec v }[/math] of the proton due to the moving proton?

Example 3

An electron located at the origin is moving with velocity [math]\displaystyle{ \vec velectron }[/math] in the +z direction. A proton is located directly in front of the electron and is moving with a velocity [math]\displaystyle{ \vec vproton }[/math] in the -y direction. What is the magnetic field at the location of the proton due to the moving electron?

Answers to Examples

Example 1:

First, calculate [math]\displaystyle{ \vec r }[/math], which is [math]\displaystyle{ \vec r = \lt 200, -300, 0\gt -\lt 0,0,0\gt =\lt 200, -300, 0\gt }[/math] m. Using [math]\displaystyle{ \vec r }[/math], calculate [math]\displaystyle{ \hat r }[/math]: [math]\displaystyle{ \hat r = \frac{ \lt 200, -300, 0\gt }{\sqrt {200^2 + -300^2}}= \lt 0.554, -0.832, 0\gt }[/math]

Next, calculate [math]\displaystyle{ q \vec v }[/math]. Remember that an electron carries a negative charge: [math]\displaystyle{ -1.6e-19* \lt 2e8, 0, 0\gt = \lt -3.2e-11, 0, 0\gt }[/math]. Next, compute the cross product, [math]\displaystyle{ q\vec v\times\hat r }[/math]. The cross product is given as [math]\displaystyle{ \vec A\times\vec B = \lt AxBz - AzBy, AzBx - AxBz, AxBy-AyBz\gt }[/math] or by computing the determinant. The cross product in this case is [math]\displaystyle{ \lt 0, 0, 2.65e-11\gt }[/math].

Finally, divide [math]\displaystyle{ q\vec v\times\hat r }[/math] by the magnitude of [math]\displaystyle{ \vec r }[/math] squared: [math]\displaystyle{ \frac{ \lt 0, 0, 2.65e-11\gt }{360.55} = \lt 0, 0, 7.34e-14\gt }[/math]. Multiply by the constant [math]\displaystyle{ 1e-7 }[/math] given in the formula, and the final answer is [math]\displaystyle{ \vec B = \lt 0, 0, 7.34e-21\gt Teslas }[/math]

Example 2:

First, as in example one, calculate [math]\displaystyle{ \vec r }[/math], and then the magnitude of [math]\displaystyle{ \vec r }[/math]. [math]\displaystyle{ \vec r = \lt 0, 0, z\gt - \lt x, 0, 0\gt = \lt -x, 0, z\gt }[/math]. The magnitude of [math]\displaystyle{ \vec r }[/math] is then [math]\displaystyle{ \sqrt{x^2 + z^2} }[/math]. We can then multiply the magnitudes of [math]\displaystyle{ q,\vec v, }[/math] [math]\displaystyle{ \sin(theta) }[/math] to get the final answer:

[math]\displaystyle{ B = \frac{\mu_0}{4\pi}\frac{qvsin(34)}{(\sqrt{x^2 + z^2})^2} }[/math]

Example 3:

As seen in the diagram, [math]\displaystyle{ \hat r }[/math] from the proton to the electron is parallel to the electron's velocity. Therefore, [math]\displaystyle{ \vec velectron\times\hat r }[/math] is zero.

Applications

Magnetic Response

The Biot-Savart law has applications in nuclear magnetic resonance (NMR) spectroscopy, used to measure the chemical signals given off by compounds. The law can be used to calculate the magnetic responses at the atomic or molecular level, provided that the current density can be obtained mathematically. For more about NMR spectroscopy, see the wiki page [5]

In this example,[2], the yellow arms represent whirring space from a black hole and the red lines represent vortex lines. Astrophysicists may use the Biot-Savart Law to calculate the velocity.

Aerodynamics

In aerodynamics, the Biot-Savart law may be used to calculate the velocity induced by vortex lines, which are lines that are everywhere tangent to the vorticity vector. A vorticity vector is a pseudovector field that describes the tendency of something to rotate, in other words, the curl of the velocity field of a fluid.

Medical Technology

Aside from applications in aerospace engineering and chemistry, the Biot-Savart law also plays an important role in MRI imaging techniques. It's important to understand how a looped wire can create a current so these technologies can be as accurate as possible without harming patients who receive them.

History

Felix Savart was born on June 30, 1791 in Mezieres, France to a family with a strong association with military engineering schools. While completing his formal education in 1808 at the university in Metz, Savart decided to pursue medicine and become a physician. After serving a short stint in Napoleon's army in the the first engineering battalion, he resumed his medical training and graduated from Strasbourg in 1816. During his medical studies, Savart became interested in first century Roman writer Aulus Cornelius Celsus and his famous medical book De medicinia. Savart began working on a translation and set up a medical practice in Metz in 1817, but gradually became more interested in physics than patients, particularly in sound and acoustics. He began building violins as a way to explore the form of the instrument through mathematical principles.

In 1819, Savart officially closed the doors of his medical practice and went to Paris to find a publisher for the translation of De medicina. While there, he attended a lecture on acoustics at by Jean-Baptiste Biot at the Faculty of Sciences. The two met there and began collaboration, when in 1820, Hans Christian Oersted published that a compass needle placed near a wire carrying current pointed at right angles to the wire. Biot and Savart began looking more closely into the field produced by a wire, and by using the oscillation of a magnetic dipole to determine the strength of the field close to a wire carrying current, they discovered what is now called the Biot-Savart Law [[6]].

References

This section contains the the references you used while writing this page

@@ Line 9: / Line 9: @@
 The general formula for a single charge is <math>\vec B=\frac{\mu_0}{4\pi}\frac{q\vec v\times\hat r}{r^2} </math> where <math> \mu_0 </math> is the constant <math> 1e-7 \frac{tesla * m^2}{coloumb * \frac{m}{s}} </math> exactly. <math> \vec v </math> is the velocity of the point charge <math> q </math>, and <math> \hat r </math> is the unit vector pointing from the source location towards the observation location ('''remember''' <math> r= r(obs)-r(source) </math>)
 '''Direction of Magnetic Field'''
 The direction of the magnetic field is not as simple as the direction of an electric field. The magnetic field's direction is given by crossing the velocity vector with the <math> \hat r </math> vector. The product of crossing two vectors is '''always''' a vector perpendicular to both of the original vectors! The cross product is at a maximum when the angle between the two vectors equals ninety degrees. The cross product is '''zero''' when two vectors are parallel to one another (the angle between the two vectors equals zero or 180).
-'''A special note:''' When dealing with a moving electron, be sure to take into account the negative charge on the electron; this negative charge will switch the sign of the cross prodcut between <math> \vec v </math> and <math> \hat r </math>
+'''A Special Note:''' When dealing with a moving electron, be sure to take into account the negative charge on the electron; this negative charge will switch the sign of the cross product between <math> \vec v </math> and <math> \hat r </math>.
 '''Magnitude of Magnetic Field'''