Electric Potential Difference

Claimed by Daniel Kurniawan

L0

Electric Potential Difference, otherwise known as Voltage, is the difference in electric potential energy between two points per unit of electric charge. The voltage between two points is equal to the work done per unit of charge against a static electric field to move the test charge between two points and is measured in units of volts.

Voltage can be caused by static electric fields, by electric current through a magnetic field, by time-varying magnetic fields, or some combination of these three. One can use a voltmeter to measure the potential difference between two points in a circuit. A voltage may represent either a source of energy (electromotive force), or lost, used, or stored energy (potential drop).

Voltage

Definition

Say you have two points "A" and "B" in space. The potential difference is defined as the difference in electric potential between those two points. Electric potential is electric potential energy per unit charge, measured in joules per coulomb, otherwise known as volts.

Calculating Potential Difference

[math]\displaystyle{ \Delta V_{BA} = V(x_B) - V(x_A) = - \int_{r_0}^{x_B} \vec{E} \cdot d\vec{l} - \left( - \int_{r_0}^{x_A} \vec{E} \cdot d\vec{l} \right) = \int_{x_B}^{r_0} \vec{E} \cdot d\vec{l} + \int_{r_0}^{x_A} \vec{E} \cdot d\vec{l} = \int_{x_B}^{x_A} \vec{E} \cdot d\vec{l} }[/math]

As stated above, the potential difference from one point to another in space is calculated as the line integral of the electric field and the time rate of change of magnetic field along that path (alternate way - multiply electric field times the distance covered across the two points). The voltage between point A to point B is equal to the work which would have to be done, per unit charge, against or by the electric field to move the charge from A to B. The voltage between the two ends of a path is the total energy required to move a small electric charge along that path, divided by the magnitude of the charge. Both an unchanging electric field and a dynamic electromagnetic field must be included in determining the voltage between two points.

Potential difference is defined in such a way that negatively charged objects are pulled towards higher voltages, while positively charged objects are pulled towards lower voltages. This means that the conventional current in a always flows from higher voltage to lower voltage. Current can flow from lower voltage to higher voltage, but only when a source of energy is present to push it against the opposing electric field. For example, inside a battery, chemical reactions provide the energy needed for ion current to flow from the negative to the positive terminal.

Applications

Circuits

Potential difference is typically used in describing the voltage dropped across some sort of electrical device, such as a resistor. The voltage drop across the device is the difference between measurements at each terminal of the device with respect to a common reference point. The voltage drop is the difference between the two readings. Two points in an electric circuit that are connected by an ideal conductor without resistance and not within a changing magnetic field have a voltage of zero. Any two points with the same potential may be connected by a conductor and no current will flow between them.

Kirchoff's Circuit Laws

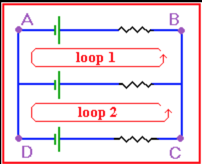
Kirchoff's Circuit Laws are used to calculate the various voltages within a circuit. For example, the voltage between points A and C is the sum of the voltage between A and B and the voltage between B and C. The various voltages can be calculated using Kirchoff's Voltage Law, which states that the directed sum of the electrical potential differences around any closed network is zero. Essentially, the sum of the potential differences in any closed loop is equivalent to the sum of the potential drops in that loop.

[math]\displaystyle{ \sum_{k=1}^n V_k = 0 }[/math]

Example

In the figure above, the total voltage around loop 1 should sum to zero, as does the total voltage in loop 2. Also, the loop which consists of the outer part of the circuit (the path ABCD) should also sum to zero, as shown by Kirchoff's Voltage Law.

See Also

Kirchoff's Circuit Laws Alternating Current Direct Current Electric Potential

Ohm's Law

External Readings

Kirchoff's Voltage Law

Electric Potential Difference

YouTube Videos

Calculating Potential, Potential Difference, and Voltage

Potential Difference as a Path Integral

References

Voltage Potential Difference

Potential and Potential Difference